CS 591 Fall 2018: Iterative Methods for Graph Algorithms and Network Analysis
Lectures: T,Th 12.30-1.45p min MCS B23.
Instructor: Prof. Lorenzo Orecchia, MCS 135D. Office hours: by appointment
Announcements
See you in class!
Lecture Notes
| Date | Topic | Overleaf Link |
| 9/4 | Graph Matrices, Linear Algebra Review | Previous year scribes |
| 9/6 | Linear Algebra Review, Spectral Theorem | Previous year scribes |
| 9/11 | Averaging and the Natural Random Walk: Why the Laplacian? | Erasmo's notes |
| 9/13 | The Spectral Gap and the Convergence of Random Walks? | In progress |
| 9 /18 | More on 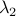 | Erasmo's notes : Previous year scribes |
| 9/20 | Intro to Graph and Matrix Sparsification | Erasmo's notes |
| 9/25 | Sparsification Wrap-up | Erasmo's notes |
| 9/27 | Graph Cuts and Spectral gap | Erasmo's notes : Previous year scribes |
| 10/2 | Metric Embeddings | Erasmo's notes: Previous year scribes |
| 10/4 | Class Cancelled | |
| 10/11 | Cheeger's Inequality | Erasmo's Notes |
| 10/16 | Flow-based Graph Partitioning: Leighton-Rao | Erasmo's notes |
| 10/18 | LR Rounding | Erasmo's notes : Previous year scribes |
| 10/23 | Semidefinite Programming | Erasmo's notes |
| 10/25 | Vector Programming via SDPs: Maxcut Relaxations | Erasmo's notes |
| 10/30 | Maxcut SDP Rounding. Balanced Partitioning SDP | Erasmo's notes |
| 11/ 1 | Effective Resistance and PageRank: An SDP View | Erasmo's notes |
Course Information
Course Outline: Iterative methods allow us to trade-off precision and running time to produce theoretically sound, fast algorithms for many optimization problems. These methods rely on a very “continuous” interpretation of the problem, incorporating techniques such as steepest-descent and coordinate descent that strongly rely on geometric intuition. In this class, we will turn this perspective on his head and show that iterative methods can be extremely useful in understanding and efficiently solving fundamental combinatorial problems on graphs, a characteristically discrete structure. This has important implications at a time when input graphs may have even billions of nodes and any super-linear running time is practically infeasible.
Tentative Syllabus: The following topics will be covered:
Spectral Graph Theory I: Graph Matrices and Graph Eigenvalues;
Spectral Graph Theory II: Random Walks over Graphs, Graph Partitioning, Spectral Clustering;
Iterative Methods I: Electrical Circuits as Graphs: Laplacian systems, Preconditioning, Fast Solvers
Iterative Methods II: Graph Sparsification
Course Policies
Prerequisites
While the class will not depend heavily on background material, it will require familiarity with fundamental algorithmic problems and techniques at the level of CS330 or equivalent. A working knowledge of basic linear algebra is also required. Do not hesitate to contact me if you are not sure whether your previous preparation will allow you to benefit from the class.
Workload
There will be three components to the workload in this class: scribing, homework and final exam.
- Scribing
Thanks to students in previous years, I have good latex notes for about 70% of the course. When we get to the new new material, I will ask 1 or 2 students to scribe for each lecture. These students are expected to collaborate to produce high-quality lecture notes in Latex through the collaborative Latex editor overleaf.com. The scribes should submit a final draft of their notes within 5 days of the class. The quality and clarity of the notes will be part of the evaluation. No student will be asked to scribe more than once
- Homework
There will be 2 homework assignments. You are encouraged to collaborate on the solution of the homeworks, but you must write up your own answers. If you do collaborate, you must acknowledge your collaborators.
- Final Exam
This will be a take-home exam, on which collaboration is not allowed.
In the homework and the exam, you may rely on published or online material, but you must acknowledge your sources.
Evaluation
The grading will roughly work out as follows: Scribing 15%, Homeworks 35% and Final 50%.