CS 112 Lab 10: Depth first search in Graphs

Graph representation

We will use an adjacency matrix represention for a graph. An example graph with its adjacency matrix is shown below. Each row (and column) of the adjacency matrix corresponds to a node in the graph. An entry (i,j) is 1 if node i is connected to node j.

Note that our adjacency matrix is symmetric about the main diagonal. The diagonal entries are zero since a node is assumed not to be connected to itself. These two conditions are not strictly neccessary for general graphs but assumed here for simplicity.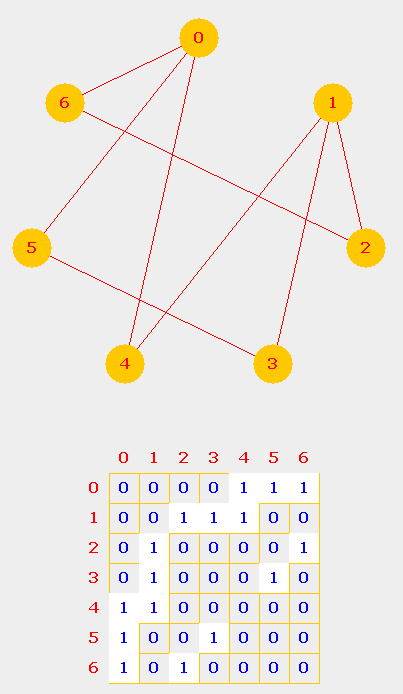

Each row (and column) of the adjacency matrix corresponds to a node in the graph.
An entry (i,j) is 1 if node i is connected to node j.

Depth First Search (DFS)

Similar to the preorder travesal for trees, we can define DFS traversal for a graph. In a graph, no special node is identified as a root. A DFS traversal can hence be initiated from any node of the graph. The figures below illustrate DFS traversals on the above graph starting from two different nodes 0 & 3.

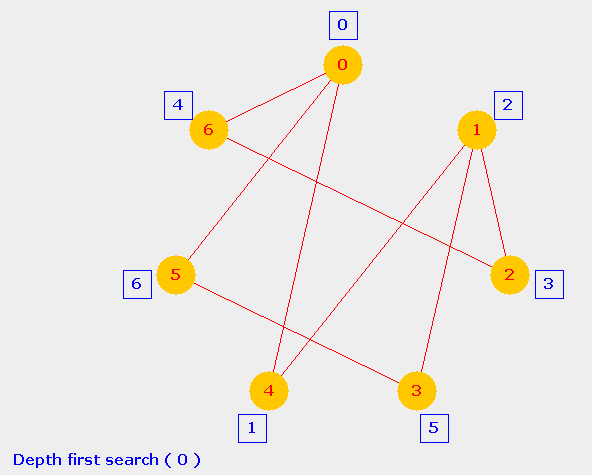The DFS traversal sequence initiated from node 0 is shown adjacent to each node.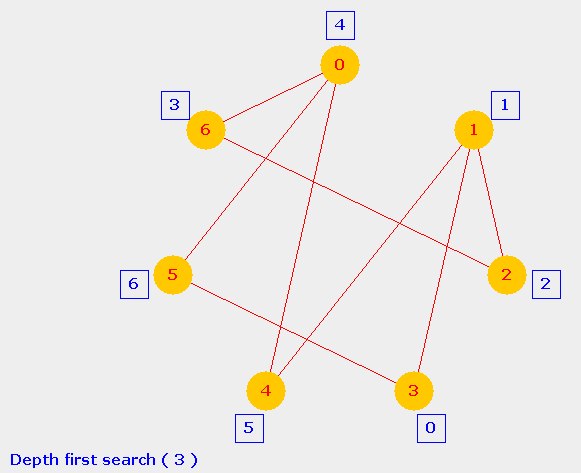


DFS traversal sequence initiated from node 3 is shown adjacent to each node.

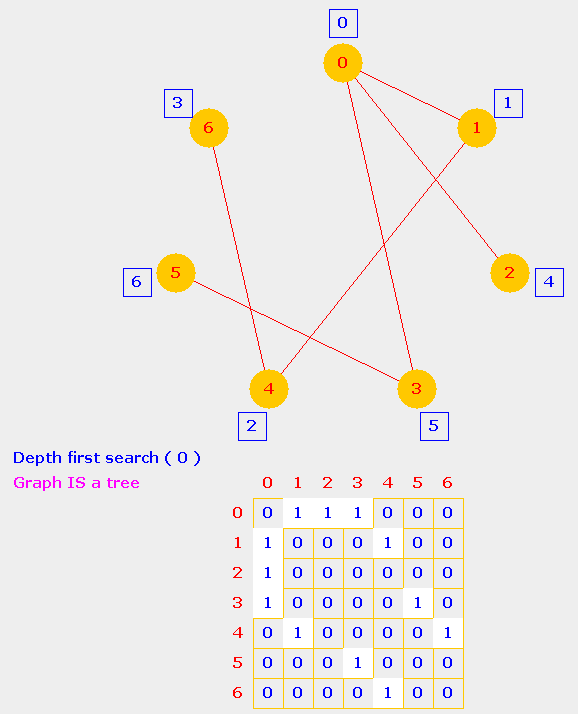
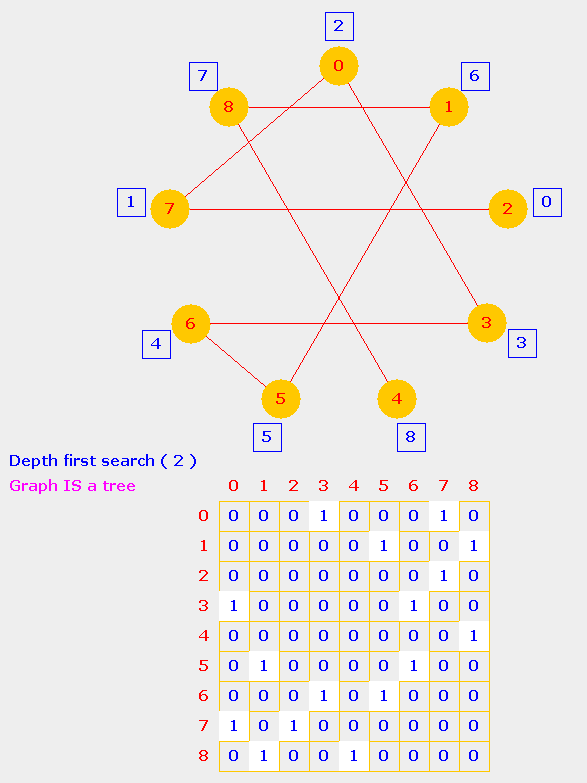
An DFS application: When is a given graph a tree?

A graph that satisfies following two conditions is a tree.

• The graph should not have any cycles (i.e., the graph should not contain any loops).
  The above graph for instance has three cycles, two of them being
  (0->6->2->1->4->0) and (0->5->3->1->4->0). Can you spot the third cycle? This graph is clearly not a tree.
  
  
• The graph should be fully conneceted. This implies that starting from any node we should be able to reach all nodes in the the graph. The above example satisifies this property since every node is reachable from any node we pick.

Both the properties can be checked by perfoming a DFS traversal on the graph,

• If during a DFS traversal starting from any node (say node 0), we find that the current node has a child that was already visited, we have found a cycle in the graph. We return not a tree.
  
  
• If the above DFS travesal completes without finding any cycles we need to check if there are nodes in the graph that were never visited. If we find such nodes, the graph is not fully connected and hence is not a tree.

A graph that satisifies both conditions is a tree. Examples of graphs that are also trees are shown below. The second one is in fact a one-dimensional chain.

Download class files for the lab below,

• DFS.java
  
  Contains an adjacency matrix based implementation of a graph data structure. This class has two unfinished methods, doDfsRecursive() and checkCycleViaDFS(). The TF will help you complete the first method, the second is method is your task for today.
  
  Task: follow TF to complete doDfsRecursive() method, then complete the checkCycleViaDFS() method.
  
  
• Main.java
  
  This is our client class to test DFS. It open a graphics window to display the graph.
  

http://cs-people.bu.edu/tvashwin/cs112_spring08/lab10.html

DFS.java