Problem Definition
In this project, we use techniques of computer vision to find out vehicles on videos that captured from common roads, track the vehicles' traces and calculate the velocity and numbers of the cars in the video.
Method and Implementation
We use Harris Corner Detector to find out cars in the video, then, we use Kalman filter and Hungarian algorithm to track the traces of each car, and finally
use the knowledge of camera calibration to help calculating the velocity of our tracked vehicles
the program consists of four parts: main, tracker corner detection and helper. For the main part, we use it to combine other three parts to implement the main flow of our program.
For the tracker part, it contains three parts: Ctracker;HungarianAlg;Kalman. We use tracker part to establish a tracker to track traces of cars founded by corner detection
and use Kalman filter and Hungarian Algorithm to finish its prediction and matching
For the helper part, it mainly contains encapsulated functions to get or show the our tracking result, such as getting last position of points in a trace, drawing lines of traces in the target image
Briefly outline the functions you created in your code to carry out your algorithmic steps described above.
Discussion
- 1.The Main Work Flow of the Program
- (1)Detect cars on the video.
- (2)Use Kalman filter and Hungarian algorithm to track cars.
- (3)Use camera calibration to calculate the speed of each car. Count the number of cars in the video.
- (4)Show the result and write data on a .csv file.
The four steps will be repeatedly done for each frame.This is a work flow mainly inspired by fore-part of [1]. But we do it differently in some problems, as shown in the follow. As there are two directions for the road in the image, we do two tracking and calculation on them separatlely. The following discussion will mainly focus on one of them.
- 2.Corner detection for vehicles
- (1)Detect cars corners by using "Harris Corner Detector"
- (2)Contract corners that are close to each other
- (3)Erase irrelevant points according to their position
we use an encapsulated "Harris Corner Detection" in opencv to detect instead of "looking for points in the image, I, where the rank of the windowed second moment matrix, rI.rIT. is two" on our own. After corner detection, we find points that are likely to be "corner" of objects in the image. As "corners" of a car should be close to each other, we contract corner points that are close to each other by calculating the middle point of two close points as result of contraction and erase the two points in the vector afterwards, so now car will be represented by the middle points of all close corner points of that car. The reason why we use corner detection instead of other methods are explained in [1], briefly, corner detection is a way of feature based tracking. The advantages of feature based tracking include: avoid influences of objects occlusion becasue some feature remain when occlusion occurs; the same algorithm can be used for tracking in daylight, twilight or night-time conditions, since some car features are distinguishable under different lighting conditions;it is self-regulating because it selects the most salient features under the given conditions. Such detection method also has its flaws, such as it will consider two car as one if they get too close. That's the reason why we don't use background subtraction, active contour and other algorithms but simply use corner detection. Lastly, as corner recognition can't distinguish which points belong to cars and which don't,we will remove some irrelevant points that are not cars' corners, such as "corners" of trees and bridge, which are near the edge of our image, we can remove them by limiting our points can only be selected when they are in a relatively "central" area.
- 3.Car tracking
- (1)If tracker data is not initialized, initialize it.
- (2)find the match of cars using Hungarian algorithm.
- (3)Use the match to update cars' traces in our tracker.
In the first frame, we have no data in our tracker, so, we use the points found in frame 0 to initialize our car tracker. Then, for corner point set in each frame, we calculate the cost(distance)matrix of the car point set and then implement Hungarian algorithm and kuhn-munkres algorithm to find their max match while keeping the sum of distance as small as possible, after that,we add new "car" and new trace in the tracker, eliminating missing "car" and their traces in the tracker and updating new position of the remaining "cars" for their traces according to the new observed position or predicting it by using Kalman filter if the observation fails. In this point, we successfully track our cars in each frame. The good handside of using Kalman filter and Hungarian algorithm to do object tracking is that they can "connect" two close points in two frame for tracking and "supplement" a predicted point if points are missing in some frames. This makes the trace of our car continuous and make it possible to calculate the velocity of a car. However, simply apply these two algorithms will make some cases worse, such as making a "car" trace take a "U turn" in the video because it finds a corresponding point match backwards or keep the trace of a car "crashing out of the road" because it can't find a corresponding point match during its "assumed existing" frames. Moreover, it can even jump from one car to another if it finds a corresponding point in another car. The difference of our program and [1] is that they set an exit zone to erase missing cars, but we do it by judging whether the trace can't find its corresponding point for a certain amount of frames. But we set our enter zone just like them, to eliminate the traces that occurs in the middle of the driveway as it is impossible to happen.
- 4. use calibration procedure to calculate the real velocity of cars
- (1)Use formula mentioned in [2] to convert image coordinate to its world coordinate.
- (2)Calculate the instantaneous velocity of the car. We found some related paper to convert the image coordinate into a real world coordinate. And we find the case from [2] is similar to ours and can be used to compute our world coordinate for cars, the formula is show as below:
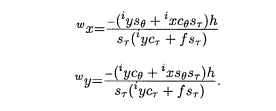
The reason for why we use this formula instead of using simple equation are: 1. the road we capture is not horizontal or perpendicular to our image, it has angle about our x-axis so we need to take the angle theta into consideration. 2. We photo the driveway in a higher place. As a result, the car "seems" to move faster when they are closer to the camera and we also need to consider an angle tau for the height we took the video. After implementing the formula from [2], the velocity of our cars can remain 50-80 in our image, which is far more better than using a simple linear equation, although it look rather unstable from our result. The unit of our velocity is not determined, but it can be easily calculated if we measure the distance or look up for some certain length data between objects(such as the road's length or car's size).
Evaluation
Confusion Matrix
|
|
Positive | Negative |
| True |
25 |
0 |
| False |
7 |
7 |
Accurate = (TN + TP) / N + P = 25 / 39 ≈ 0.7
Sensitive = TP / P = 25 / 32 ≈ 0.8
Specific = TN / N = 0
Precise = TP / TN + FP = 25 / 32 ≈ 0.8
Recall = TP / TN + FN = 25 / 32 ≈ 0.8
-
5.Future work:
- (1)Eventually we do some tracking of cars in our video. But we still don't have time to play with them, so we may use this program to do funny analysis on the video, such as judging whether there's a traffic jam when no car has a higher speed than a threshold, or judging whether there's a car drive too fast as its speed is continuously much higher than others. (2)Also, we should optimize our program, for example, make the trace of our cars more precise.
*.Further discussion: Objects Matching in two Frames
Muti-object tracking involves with the assignment problem of the detected objects. In our project, we use Hungarian algorithm to estimate the association of detections from one frame to the next frame.(As shown in Figure 1) In general, the Hungarian Algorithm is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.
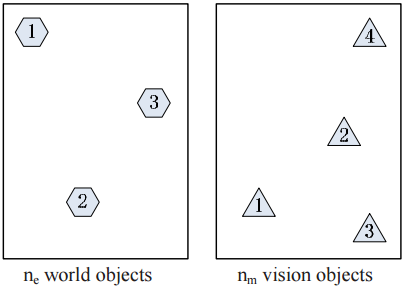
Figure 1 Continuous Frame
In our case, the matching problem can be regarded as a perfect matching with min-cost problem in our defining weighted bipartite graph. Specifically, after corner detection, we got several points to represent each vehicles, so we can transfer the detected point sets in continuous two frames into a weighted bipartite graph by calculating the distance between linked points. (Here we assume that the points in set A are all linked with the points in Set B), and in our method, we call this matrix the Cost Matrix, and then we use the Hungarian Matrix to manipulate the cost matrix by starring and priming zeros and by covering and uncovering rows and columns, which can be divided into the following steps:
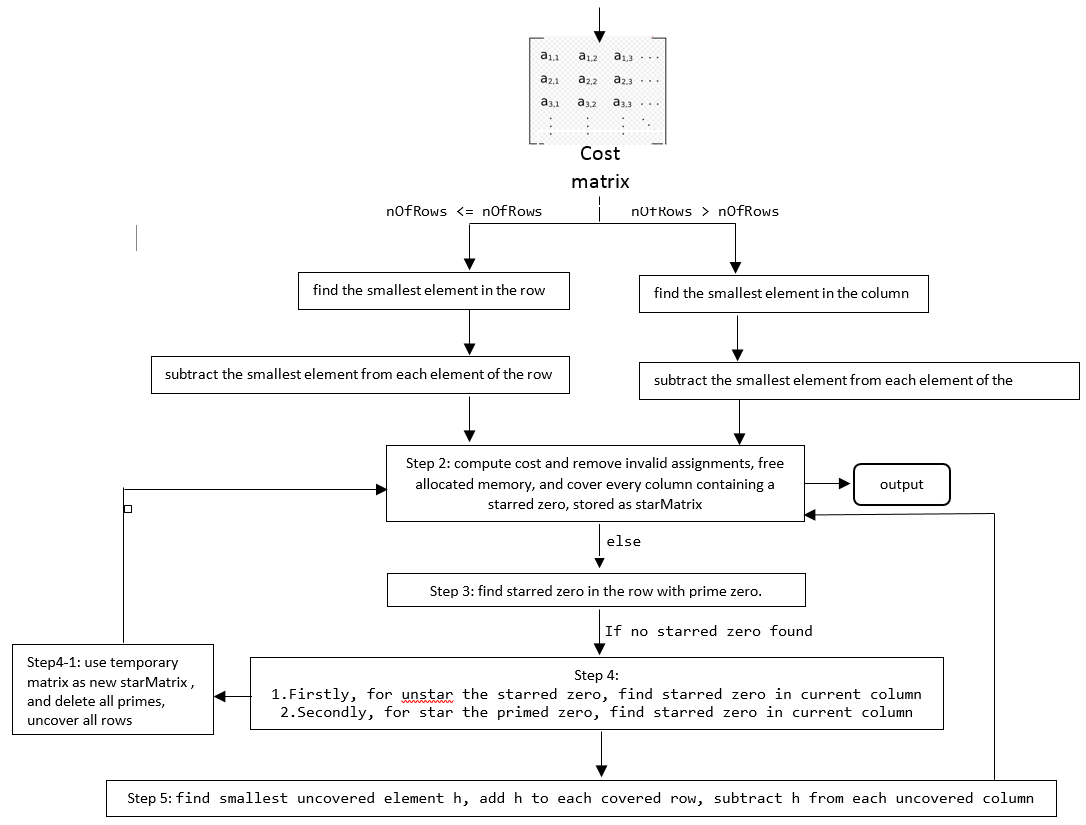
Figure 2 Hungarian Algorithm
- Kalman Filter :
After the calculation of Hungarian algorithm, we have a matching matrix which implies which object is the one in the last frame, then we need to update the data in the single traces (push new points into he traces). In this part, I build a Kalman Filter class for the project, and initialize the processing covariance and the measurement covariance relatively large[because, although not sure, I try to make the Kalman Filter trust more on the measurement(points by corner detection) rather than the predictions(because at the very beginning it is kind of mess)].
And, in the updating part, let’s say for the trace, if there is a point well matched, which is ideal, we would take the point as our next point and make a correction using Kalman Filter with the prediction and the matched point, then push the new point into the corresponding trace point vector; Otherwise, while there is not such a matched point, we would use the prediction produced by Kalman Filter as our new match and push it back to the trace vector(will count such unmatched frames, and delete the trace if there are too many frames unmatched). - Calculating Velocity:

Now we get the traces which are stored as vector of points,now we should be able to calculate the vehicles' velocities.However, the vehicles happen to move closer and closer to my teamate who took the video,which make it difficult to calculate the velocities directly.So, here we use the method in the paperBas, E.K.,& Crisman,J.D. (1997).An easy to install camera calibration for traffic monitoring. to transfer the points in the camera image into points in real world.Here are some equations in the paper:
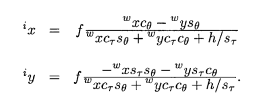
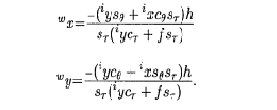
Result
| Original Step |
|
|
| Next step |
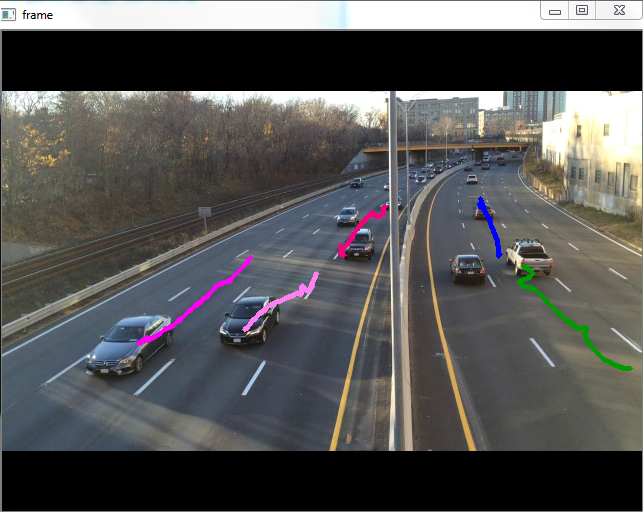
|
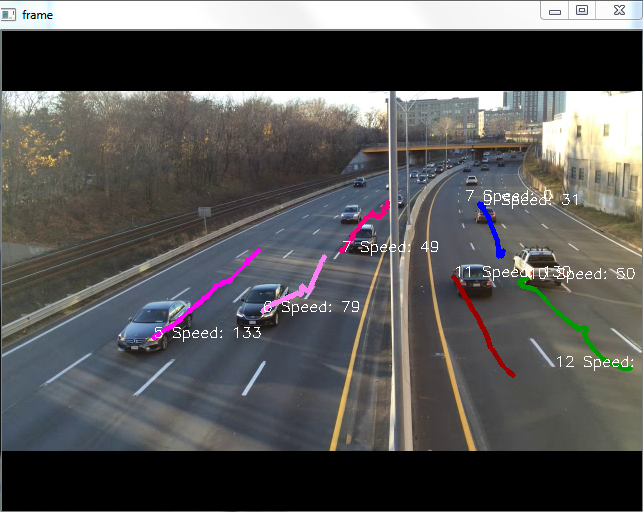
|
Conclusions
By using corner detection, we can distinguish cars on our image and effectively avoid some occlusion and lighting problems. By using Kalman filter and Hungarian algorithm, we can detect a large part of cars that move across the image. However, these two methods will also bring errors respectively due to their limitation, we need to do some modifications on them so as to lower their negative influences.
Credits and Bibliography
[1]Benjamin Coifman, David Beymer, Philip McLauchlan, and Jitendra Malik. A real-time computer vision system for vehicle tracking and traffic surveillance. Transportation Research Part C: Emerging Technologies, 6(4):271 – 288, 1998.[2]Bas and Crisman, 1997 Bas, E.K., & Crisman, J.D. (1997). An easy to install camera calibration for traffic monitoring. Proceedings of IEEE Conference on Intelligent Transportation System, Boston, Massachusetts,.(pp. 362-366).
[3]Lütteke, Felix, Xu Zhang, and Jörg Franke. "Implementation of the hungarian method for object tracking on a camera monitored transportation system." Robotics; Proceedings of ROBOTIK 2012; 7th German Conference on. VDE, 2012.
[4]J. Munkres, "Algorithms for the Assignment and Transportation Problems," Journal of the Society for Industrial and Applied Mathematics, Vol. 5, No. 1, pp. 32-38, 1957.
Code References: MultipleObjectTracking: https://github.com/Smorodov/Multitarget-tracker
