Assignment 4: More practice with functions

Assignment 4: More practice with functions
- Preliminaries

due by 9:00 p.m. EST on Tuesday 2/4/25

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

For each problem in this problem set, we will be writing or evaluating some Python code. You are encouraged to use the Spyder IDE which will be discussed/presented in class, but you are welcome to use another IDE if you choose.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Programming Guidelines

Refer to the class Coding Standards for important style guidelines. The grader will be awarding/deducting points for writing code that comforms to these standards.
Every program file must begin with a descriptive header comment that includes your name, username/BU email, and a brief description of the work contained in the file.
Every function must include a descriptive docstring that explains what the function does and identifies/defines each of the parameters to the function.
Your functions must have the exact names specified below, or we won’t be able to test them. Note in particular that the case of the letters matters (all of them should be lowercase), and that some of the names include an underscore character (_).
Make sure that your functions return the specified value, rather than printing it. None of these functions should use a print statement.
If a function takes more than one input, you must keep the inputs in the order that we have specified.
You should not use any Python features that we have not discussed in class or read about in the textbook.
Your functions do not need to handle bad inputs – inputs with a type or value that doesn’t correspond to the description of the inputs provided in the problem.
You must test your work before you submit it You can prove to yourself whether it works correctly – or not – and make corrections before submission. If you need help testing your code, please ask the course staff!
Do not submit work with syntax errors. Syntax errors will cause the Gradescope autograder to fail, resulting in a grade of 0.

Warnings: Individual Work and Academic Conduct!!

This is an individual assignment. You may discuss the problem statement/requirements, Python syntax, test cases, and error messages with your classmates. However, each student must write their own code without copying or referring to other student’s work.
It is strictly forbidden to use any code that you find from online websites including but not limited to as CourseHero, Chegg, or any other sites that publish homework solutions.
It is strictly forbidden to use any generative AI (e.g., ChatGPT or any similar tools**) to write solutions for for any assignment.

Students who submit work that is not authentically their own individual work will earn a grade of 0 on this assignment and a reprimand from the office of the Dean.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Task 1: Functions for time value of money calculations

40 points; individual-only

In this task, you will implement several well-known algebraic formulas used for financial computations. These formulas are built-in to functions on the famous BA-II plus financial calculator used in finance classes, as well as in the Excel spreadsheet software used in the finance industry.

Write all of the functions for this task in the file a04_tvm.py. Remember to create a header comment at the top of your file with your name, email address, assignment number, and a brief description.

Brief Finance Background and definitions

An amount of money today can be invested, earning interest to the investor. Think of interest as the “rental fee” for money. Interest is paid by a borrower (who “rents” money now) and earned by an investor (who “rents out” money now).

The future value is the value of an investment at some time in the future, after accounting for the interest earned (paid) over that time.

The present value is the value today (in the present) of an amount to be paid or received at some time in the future, after accounting for the interest earned (paid) over that time.

We can only add or subtract cashflows that occur in the same time period. Thus, when working with cashflows that occur different time periods, it is crucial to convert all amounts into present value before doing any addition or subtraction.

An annuity is a stream of payments (cash flows) that continue for many periods, and then stops. Examples include loan payments (the same amount each month for 48 months) or regular investments to a retirement plan (e.g., saving 15% of your salary each month). Since these cash flows occur at different times, we cannot compare them directly to each other or add them together. What we can do is to find the present value of the annuity, which is a value today. Conversely, if we already know the present value, we can find the annuity payment that corresponds to that present value, spread over many periods.

Implementing the Financial Calculations

Write the function future_value(r, n, pv) to calculate and return the future value of a lump sump pv invested at the periodic rate r for n periods.

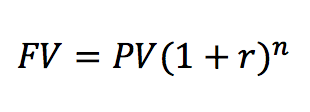
The equation for the future value of a lump sum is: FVFORUMULA

Examples:

    >>> # $100 at 5% rate for 2 years
    >>> future_value(0.05, 2, 100)
    110.25
    >>> # $400 at 8% APR for 20 years (with monthly compounding)
    >>> future_value(0.08/12, 20*12, 400)
    1970.7211083238797

Write the function present_value(r, n, fv) to calculate and return the present value of a lump sum fv to be received in the future, discounted at the periodic rate r for n periods.

The equation for the present value of a lump sum is:

PVFORUMULA

Examples:

    >>> # $1000 to be received in 5 years at 6% per year
    >>> present_value(0.06, 5, 1000)
    747.2581728660571
    >>> # $500 received in 5 years, 6% APR, semi-ann. compounding
    >>> present_value(0.06/2, 5*2, 500)
    372.0469574483625

Write the function present_value_of_annuity(r, n, pmt) to calculate and return the present value of an annuity of pmt to be received each period for n periods, discounted at the rate r.

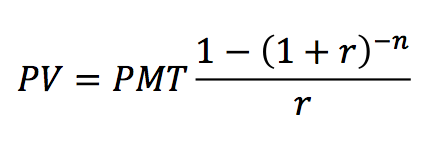
The equation for the present value of an annuity is: PVANNUITY

Examples:

    >>> # pv of 30 payments of $250 per year, 5% interest
    >>> present_value_of_annuity(0.05, 30, 250)
    3843.1127567207104
    >>> # pv of 60 payments of $471.75 per month, 0.9% APR
    >>> present_value_of_annuity(0.009/12,60, 471.75)
    27667.441596482677

Write a function annuity_payment(r, n, pv) that calculates the amortizing annuity
payment for a present value of pv to be repaid at a periodic interest rate of r for n periods.

The equation for the amortizing annuity payment is: PMT

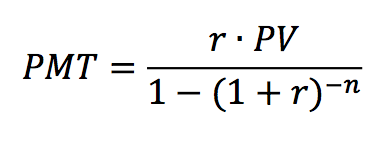
Examples:

    >>> # annuity payment for pv of $1,000 for 10 year at 5%
    >>> annuity_payment(0.05, 10, 1000)
    129.5045749654566
    >>> # annuity payment for pv of $27,667 for 60 months at 0.9% APR
    >>> annuity_payment(0.009/12, 60, 27667.44)
    471.7499727788093

Write the function dollar_format(amount) to create a formatted string representation of a numeric amount. The function must create a string, which includes the dollar sign ($) and the amount of whole dollars (without cents). For example:
```
>>> dollar_format(123.456)
'$123'
>>> dollar_format(123456.789)
'$123456'
```
Notes:
- You will need to use the conversion function int(x) (to obtain the number of whole dollars with no cents) and str(x) (to convert the number into a string representation of that number). Finally, you may use concatenation (the + operator) to join two strings together.
- Do not use print inside the dollar_format function. Rather, the function must return a string representation of the number.

Task 2: The Life-Cycle Model of Saving and Consumption

40 points; individual-only

Background/Overview

The Life-Cycle Model was first developed by Nobel Prize winning economist Franco Modigliani in the 1950s to help explain household’s decisions about spending and saving over time. Modigliani observed that households accumulate wealth (assets) during their working years and spend down that wealth during their retirement years, with the goal of maintaining a relatively smooth standard of living for all years, i.e., to keep spending the same amount year in and year out, even when they stop working.

We can calculate this sustainable (“smooth”) level of consumption using some of the time-value of money computations from Task 1:

An individual’s income from work is like an annuity: it goes on for many years, and then stops at their retirement. A person’s “human capital” is the present value of their remaining lifetime work income.
We compute a person’s total resources (“economic net worth”) is the sum of their human capital and any existing financial assets (or debts).
The smooth level of annual consumption is also like an annuity with cashflows (annual spending) that continue for life. The level of consumption is effectively an anuity payment, where the present value is the person’s economic net worth.

Assumptions

We do not know how the price level will change in the future (i.e., “inflation”). Given this unknown, we will use “real dollars” (i.e., dollars with today’s purchasing power) for all calculations.
We will also use the “real” interest rate (i.e., the interest rate that an investor would earn after accounting for inflation).
As a simplification, we assume no taxes or government benefits.

Implementation Details

Do your work in a file called a04_lcm.py. Save your file in the same directory as your file from task 1 (above). At the top of your file (after the header comment), write the following statements to be able to access the functions you wrote in task 1:

    from a04_tvm import present_value_of_annuity
    from a04_tvm import annuity_payment
    from a04_tvm import dollar_format

Write a function calculate_smooth_consumption(age_now, retirement_age, income, assets, rate), which will implement the financial calculations of the life-cycle model, and determine the sustainable smooth level of consumption for all years of life beginning now.

The parameters are:
age_now, an integer measuring whole years of age
retirement_age, an integer representing the age at retirement
income, one’s annual income (in real dollars per year)
assets, existing financial assets
, rate, the real (net of inflation) rate of return on risk-free investments.

This function will perform 2 financial calculations, produce several outputs (i.e., print statements), and return* the amount of consumption per year (a floating point number).

Here is an example of this function:
```
>>> # 23 year old, retirement at age 67, $0 of financial assets, 2% interest rate
>>> calculate_smooth_consumption(23, 67, 45000, 0, 0.02)
You have 44 working years with an annual income of $45000.
The present value of your human capital is about $1308598.
Your financial assets are: $0.
Your economic net worth is: $1308598.

Based on your resources, your sustainable annual consumption
to age 100 is $33453 per year.
To achieve this consumption, you must save $11546 per year 
during your working years.
```
The function also returns the amount of anual consumption, i.e., 33453.617868226094.

Here’s what happens inside the function:

(a) Print out the number of working years remaining and the income per year. Use your dollar_format function to obtain the dollar amounts without cents.

(b) Calculate the human capital, which is the present value of the user’s lifetime income (i.e., an annuity). Use your present_value_annuity function from above. Print out the present value of human capital, with dollar formatting.

(c) Calculate the economic net worth, which is human capital plus financial assets. Print out the economic net worth, with dollar formatting.

(d) Calculate the annual consumption (i.e., sustainable standard of living). First, determine the number of years of consumption, as 100 – age. Use the annuity_payment function (from above) to calculate the amount of annual consumption that can be sustained from the economic net worth. Print out the annual consumption.

(e) Calculate the amount of annual savings required. Savings is income minus consumption. Print out the required annual savings.

(f) Return the amount of consumption as a floating point number.

Here is a second example of this function:
```
>>> # 34 year old, retirement at age 65, $150000 of financial assets, 2% interest rate
>>> calculate_smooth_consumption(34, 65, 80000, 150000, 0.02)
You have 31 working years with an annual income of $80000.
The present value of your human capital is about $1835016.
Your financial assets are: $150000.
Your economic net worth is: $1985016.

Based on your resources, your sustainable annual consumption
to age 100 is $54431 per year.
To achieve this consumption, you must save $25568 per year 
during your working years.
```
The function also returns the amount of anual consumption, i.e., 54431.569844940794.

TEST THIS FUNCTION THOROUGHLY BEFORE PROCEEDING TO THE NEXT PART
Write a function interactive_life_cycle_model(), which will create an interactive version of this calculator. This function will interact with the user to collect inputs, and will call the calculate_smooth_consumption function from above to do the financial math and display outputs.

This function will not have a return value.

Begin by prompting the user for inputs for:

(a) the user’s age now

(b) age at retirement

(d) financial assets. If there are no assets, the user can enter 0, and if there are debts the user can enter a negative number.

(e) the rate of return on a risk-free, inflation-indexed investment

Data collected from the keyboard will always be received as a string, so you must convert it to numeric data type using the int or float functions, so that you can do arithmetic.

Once you have collected all inputs and converted to the correct types, you should proceed to call the calculate_smooth_consumption function from above to do the financial math and its display outputs.

Here are two examples to give you an idea of how this program should work:

Example 1: 22-year old, first job, $0 financial assets:

    Welcome to the Life-Cucle Financial Planning Calculator.

    Enter your age now: 22

    Enter your expected retirement age: 65

    Enter your current annual income: 45000

    Enter the value of your financial assets: 0

    Enter the risk-free, real rate of return: 0.02

    You have 43 working years with an annual income of $45000.
    The present value of your human capital is about $1289770.
    Your financial assets are: $0.
    Your economic net worth is: $1289770.

    Based on your resources, your sustainable annual consumption
    to age 100 is $32793 per year.
    To achieve this consumption, you must save $12206 per year 
    during your working years.

Example 2: 35 year-old, mid-career, with $150,000 of assets:

    Welcome to the Life-Cucle Financial Planning Calculator.

    Enter your age now: 35

    Enter your expected retirement age: 67

    Enter your current annual income: 83000

    Enter the value of your financial assets: 150000

    Enter the risk-free, real rate of return: 0.03

    You have 32 working years with an annual income of $83000.
    The present value of your human capital is about $1692267.
    Your financial assets are: $150000.
    Your economic net worth is: $1842267.

    Based on your resources, your sustainable annual consumption
    to age 100 is $64747 per year.
    To achieve this consumption, you must save $18252 per year 
    during your working years.

Running Your Program

Your interactive program will be contained in the function called interactive_life_cycle_model.
You can execute your interactive by calling that function at the bottom of the file (i.e., after the function has been defined).

The best way to do this is to write the following statement:
```
if __name__ == '__main__':

    interactive_life_cycle_model()
```
at the bottom of your file. Test that this works by running your program!
The autograder script is expecting to provide your program with exactly 5 inputs, in the order specified above. If you attempt to collect additional inputs, or attempt to collect them in a different order, it will not work.

Submitting Your Work

20 points; will be assigned by code review

Be sure to name your files correctly!

You will submit two files for this assignment: a04_tvm.py and a04_lcm.py.

When you upload the files, the autograder will test your functions/programs.

Warning: Beware of Global print statements

The autograder script cannot handle print statements in the global scope, and their inclusion causes this error:

autograder_fail

*   Why does this happen? When the autograder imports your file, the `print` 
    statement(s) execute (at import time), which causes this error.

*   You can prevent this error by not having any `print` statements in the global scope.
    Instead, create an `if __name__ == '__main__':` section at the bottom of the file, and
    put any test cases/print statements in that controlled block. For example:

        if __name__ == '__main__':

            ## put test cases here:
            print('future_value(0.05, 2, 100)', future_value(0.05, 2, 100))

*   `print` statements inside of functions do not cause this problem.

Notes:

You may resubmit multiple times, but only the last submission will be graded.