Assignment 5: Computing with Numbers and Formatted Output

due by 9:00 p.m. EST on Thursday 9/19/24

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

For each problem in this problem set, we will be writing or evaluating some Python code. You are encouraged to use the Spyder IDE which will be discussed/presented in class, but you are welcome to use another IDE if you choose.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Task 1: Formatting Numeric Values

30 points; individual-only

In this task, you will practice working with format strings, in which you substitute values into strings to be able to better control the spacing and precision of the values. Do your work for this task in a file called a05_number_format.py.

1. Write a function format_date(month, day, year) that returns a beautifully-formatted string representation of a calendar date in the form YYYY-MM-DD. The parameters month, day, year are integers, and you may assume they represent a valid date.

   Here are some examples of how this function must work:

   >>> format_date(10, 12, 2014)
   '2014-10-12'
   >>> format_date(3, 24, 2006)
   '2006-03-24'
   

   Notice in particular that the order of values is important, and that the result must include leading 0s where appropriate.

   NOTES:

   • You do not need to use any decision logic to solve this problem. Use Python’s format string with substitutions.

   • Do not print anything out. Your function must return the result as a string.

2. Write a function format_time(tm) that returns a beautifully-formatted string representation of a time measured in tm (the time in minutes, as a floating-point number).

   Here are some examples of how this function must work:

   >>> format_time(23)
   '00:23:00'
   >>> format_time(0.5)
   '00:00:30'
   >>> format_time(123.75) 
   '02:03:45'
   

   You will need several arithmetic statements to conver from tm to separate variables for hours, minutes, and seconds. In particular, you will need to separate the whole minutes from the fractional minutes, i.e., 23.5 minutes will need to be separated to 23 minutes and 30 seconds. Work out the arithmetic at the Python Interactive console, before incorporating it in this function definition.

   NOTES:

   • You do not need to use any decision logic to solve this problem. Use Python’s format string with substitutions.

   • Do not print anything out. Your function must return the result as a string.

   • You may not use the built-in time module or any other built-in modules.

Task 2: Computations for Aviation

50 points; individual-only

Background

How fast does an airplane fly? The answer depends on whether we are thinking about
its airspeed or ground speed. An airplane’s “true airspeed” is the speed at which the airplane is traveling relative to the surrounding air. An airplane’s “groundspeed” is how much distance the aircraft travels over the ground in a hour. The reason that the airspeed and ground speed are usually different depends on the wind speed and wind direction.

Consider an airplane that is traveling at 500 miles per hour (mph) true airspeed, but it is flying directly into a 100 mph headwind. The result is that the ground speed of the airplane is only 400 mph.

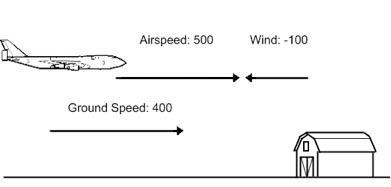
On the other hand, if the wind is blowing toward the same direction as the airplane is traveling, we would add together the true airspeed and the wind speed to find the ground speed.

It gets more complicated when the wind is blowing some different direction, e.g., at some arbitrary angle with respect to the airplane.

In aviation, the aircraft’s heading is the direction the aircraft is “aiming”, as a magnetic compas measurement in degrees from the north.

The cardinal directions are: north (0/360 degrees), east (90 degrees), south (180 degrees), and west (270 degrees).

Suppose an airplane needs to travel on a course of 45 degrees (NE), and the wind is blowing from the west (270 degrees). The wind is pushing the airplane off course, and the faster the wind is blowing, the greater the effect.

If the aircraft attempts to fly a heading of 45 degrees, it will be pushed to the to east, and ends up on an actual course that to the east of the desired heading.

To actually arrive at the desired destination, the aircraft will need to fly a heading of 22.5 degrees (NNE).

For example, suppose the aircraft course is 45 degrees, and it is flying at a true airspeed of 200 mph, with winds are out of the west (270 degrees) at 100 mph. To reach its desired target, the airplane will need to fly a heading of 22.5 degrees, and will have a ground speed of 219 mph.

In the days before digital computers, airplane pilots would use a mechanical flight computer to perform these computations. In the flight computer, we set the wind direction by turning a wheel, and then read off the ground speed:

Do your work for this task in a file called a05_aviation_calcs.py.

1. Write the function calculate_heading(course_dir, va, wind_dir, vw), that returns the heading (in degrees) that an an aircraft must navigate to reach their course direction. The paramaters are:
   the desired course direction of course_dir (degrees),
   the true airspeed of va (miles per hour),
   the direction of wind_dir (in degrees), and
   the wind speed of vw (miles per hour).
   

   The heading is the direction the aircraft must fly, to reach the desired course direction given the wind speed/direction.

   The heading is calculated as:

   

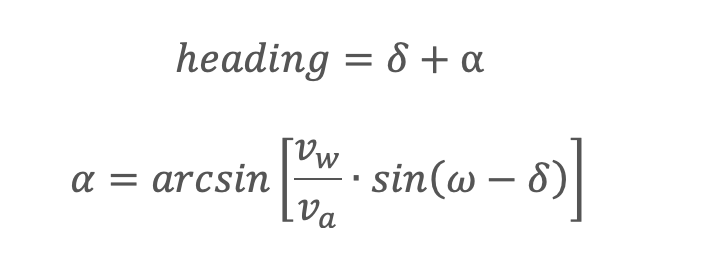
   where:
   va - True airspeed – speed of the aircraft relative to the surrounding air;
   vw - Wind speed – speed of the wind relative to the ground;
   δ - Course – desired trajectory of the flight measured clockwise from the North;
   ω - Wind direction – direction from which the air is blowing; and
   ⍺ - Wind correction angle – angle between the course and the heading (the direction to fly to compensate for the wind)
   

   Here are some examples of calculating the heading:
   
   >>> # flying east, directly into the wind
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 90, winds 100 mph
   >>> calculate_heading(90, 200, 90, 100)
   90.0 # wind does not affect this heading, flying with a tail wind
   
   >>> # flying east, with a direct tail wind
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 270, winds 100 mph
   >>> calculate_heading(90, 200, 270, 100)
   90 # wind does not affect this heading, flying directly into the wind
   
   >>> # flying east with a cross wind (from the south)
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 180, winds 100 mph
   >>> calculate_heading(90, 200, 180, 100)
   120.0
   

   Hints:

   • Remember that the math library’s trigonometry functions work in radians, not in degrees. The easiest strategy is to convert the parameters to radians, and then do all of your work in radians.

   • Break a complicated formula into parts, so you can check your work as you go. Use print statements to help debug the formulas.

   • This website has a helpful explanation as well as an interactive calculator to help you check your work.

   • Express the result as a positive number of degrees. For example, -10 degrees is the same as 350 degrees. You can accomplish this using the modulo operator (%360).

2. Write the function calculate_ground_speed(course_dir, va, wind_dir, vw) that will calculate and return the groundspeed traveled by an aircraft, given its course direction and wind conditions.

   The paramaters are:
   the desired course direction of course_dir (degrees),
   the true airspeed of va (miles per hour),
   the direction of wind_dir (in degrees), and
   the wind speed of vw (miles per hour).
   

   The calculation involves vector addition and the law of cosines. The ground speed formula in aviation is the following:

   

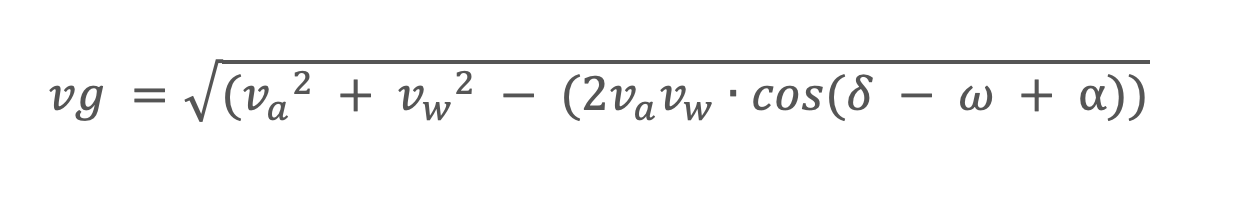
   where:
   vg - Ground speed – aircraft’s speed relative to the ground;
   va - True airspeed – speed of the aircraft relative to the surrounding air;
   vw - Wind speed – speed of the wind relative to the ground;
   δ - Course – desired trajectory of the flight measured clockwise from the North;
   ω - Wind direction – direction from which the air is blowing; and
   ⍺ - Wind correction angle – angle between the course and the heading (the direction to fly to compensate for the wind)
   

   The wind correction angle is given by:

   

   Here are some examples of calculating the ground speed:
   
   >>> # flying east, directly into the wind
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 90, winds 100 mph
   >>> calculate_ground_speed(90, 200, 90, 100)
   100.0
   
   >>> # flying east, with a direct tail wind
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 270, winds 100 mph
   >>> calculate_ground_speed(90, 200, 270, 100)
   300.0
   
   >>> # flying east with a cross wind (from the south)
   >>> # course direction 90 (east), airspeed 200 mph, wind direction 180, winds 100 mph
   >>> calculate_ground_speed(90, 200, 180, 100)
   173.20508075688772
   

   Hints:

   • Remember that the math library’s trigonometry functions work in radians, not in degrees. The easiest strategy is to convert the parameters to radians, and then do all of your work in radians.

   • Break a complicated formula into parts, so you can check your work as you go. Use print statements to help debug the formulas.

   • This website has a helpful explanation as well as an interactive calculator to help you check your work.

3. Write an interactive program in the function interactive_flight_planner(). This function will not take any parameters and it does not return any value. Instead, it will collect inputs from the keyboard, do some calculations by re-using your functions from above, and then print several outputs to the console.

   For example, suppose we are planning a flight from Boston to Seattle:

   

   Here is an example of this program, running calculations for such a flight.

   Welcome to the interactive flight planner.
   
   Enter the course direction (in degrees): 280
   
   Enter the indicated airspeed (in mph): 525
   
   Enter the wind direction (in degrees): 230
   
   Enter the wind speed (in mph): 80
   
   Enter your enroute distance (in miles): 2486
   
   Here is a summary of the program inputs:
   Course direction: 280.0 degrees, air speed: 525 mph.
   Wind direction: 230.0 degrees, wind speed: 80 mph.
   
   Given these parameters:
       Fly heading: 273.3 to stay on course.
       Ground speed will be: 470.0 mph.
   
   Enroute time is expected to be: 05:17:22.
   

   The “enroute time” is the flight time excluding taxiing out to the runway, waiting for clearance to depart, take-off and climb, descent, landing, and taxiing to the gate, which might add another 20 or more minutes on each end of the flight.

   Calculate the enroute time as distance (in miles) divided by ground speed (in miles per hours), and you will obtain a result in hours. Convert this result to minutes, and use your format_time function from Task 1 to print out a beautifully-formatted output.

   Note: an actual flight from Boston to Seattle does not flight a “straight” heading. This is because the shortest distance between two points on a sphere is an arc. Transcontinental or international flights take advantage of the arcs to shorten the travel time and fuel requirements. The actual route would require many calculations of heading between different waypoints, and the wind conditions are likely different at different times along the way... so this is a reasonable simplification.

Submitting Your Work

20 points; will be assigned by code review

Log in to GradeScope to submit your work.

Be sure to name your files correctly!

You will submit two files for this assignment: a05_number_format.py and a05_aviation_calcs.py.

When you upload the files, the autograder will test your functions/programs.

*   Why does this happen? When the autograder imports your file, the `print` 
    statement(s) execute (at import time), which causes this error.

*   You can prevent this error by not having any `print` statements in the global scope.
    Instead, create an `if __name__ == '__main__':` section at the bottom of the file, and
    put any test cases/print statements in that controlled block. For example:

        if __name__ == '__main__':

            ## put test cases here:
            print('calculate_ground_speed(200, 90, 100, 90)', 
                calculate_ground_speed(200, 90, 100, 90) )


*   `print` statements inside of functions do not cause this problem.

Notes:

• You may resubmit multiple times, but only the last submission will be graded.