Problem Set 13: Final Project, part 2: Comparing Search Algorithms

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

For each problem in this problem set, we will be writing or evaluating some Python code. You are encouraged to use the Spyder IDE which will be discussed/presented in class, but you are welcome to use another IDE if you choose.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Project Overview

As discussed in class, many problems can be framed as a search for a series of actions that take you from some initial state to some goal state. Examples include robot navigation, route finding, and map labeling. For such a problem, the state space of the problem is the collection of all states that can be reached by starting in the initial state and applying some number of actions. State-space search is the technical term given to the process of searching through the state space for a path to the goal state, and many different algorithms have been developed for that process.

The project involves applying state-space search to a classic problem known as the Eight Puzzle, which we’ve discussed in class. The Eight Puzzle is a 3x3 grid containing 8 numbered tiles and one empty or blank cell. Here is one possible configuration of the tiles, with the blank cell shown shaded blue:

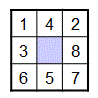
Tiles that are adjacent to the blank cell can move into that position in the grid, and solving the puzzle involves moving the tiles until you reach the following goal state:

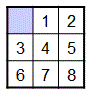
In this project, you will apply state-space search to solve any valid initial configuration of the Eight Puzzle.

Some parts of the project will be required – including an implementation of several classic state-space algorithms – but other parts will be left to your creativity. In particular, you will see that some initial configurations of the Eight Puzzle – ones that require a large number of moves – can be difficult to solve in a reasonable amount of time, and you will be encouraged to develop variations on the required algorithms that will reduce the time needed to find a solution!

Project Description

Part IV: Subclasses for other search algorithms

In this part of the assignment you will continue from the work you have done for [Problem Set 12][ps12] and implement other state-space search algorithms by defining classes for new types of searcher objects.

Uninformed state-space search: BFS and DFS

1. In searcher.py, define a class called BFSearcher for searcher objects that perform breadth-first search (BFS) instead of random search. As discussed in class, BFS involves always choosing one the untested states that has the smallest depth (i.e., the smallest number of moves from the initial state).

   This class should be a subclass of the Searcher class that you implemented in [Part III][partIII], and you should take full advantage of inheritance. In particular, you should not need to include any attributes in your BFSearcher class, because all of the necessary attributes will be inherited from Searcher.

   Similarly, you should not need to define many methods, because most of necessary functionality is already provided in the methods that are inherited from Searcher.

   However, you will need to do the following:

   1. Make sure that your class header specifies that BFSearcher inherits from Searcher.

   2. Because all of the attributes of a BFSearcher are inherited from Searcher, you will not need to define a constructor for this class. Rather, we can just use the constructor that is inherited from Searcher.

   3. Write a method next_state(self) that overrides (i.e., replaces) the next_state method that is inherited from Searcher. Rather than choosing at random from the list of untested states, this version of next_state should follow FIFO (first-in first-out) ordering – choosing the state that has been in the list the longest. In class, we discussed why this leads to breadth-first search. As with the original version of next_state, this version should remove the chosen state from the list of untested states before returning it.

   Examples:

   >>> b = Board('142358607')       
   >>> s = State(b, None, 'init')
   >>> s
   142358607-init-0
   >>> bfs = BFSearcher(-1)
   >>> bfs.add_state(s)
   >>> bfs.next_state()     # remove the initial state
   142358607-init-0
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> bfs.add_states(succ)
   >>> bfs.next_state()
   142308657-up-1
   >>> bfs.next_state()
   142358067-left-1
   

2. In searcher.py, define a class called DFSearcher for searcher objects that perform depth-first search (DFS) instead of random search. As discussed in class, DFS involves always choosing one the untested states that has the largest depth (i.e., the largest number of moves from the initial state).

   DFS, the next state to be tested should be one of the ones that has the largest depth in the state-space search tree.

   Here again, the class should be a subclass of the Searcher class, and you should take full advantage of inheritance. The necessary steps are very similar to the ones that you took for BFSearcher, but the next_state() method should follow LIFO (last-in first-out) ordering – choosing the state that was most recently added to the list.

   Examples:

   >>> b = Board('142358607')       
   >>> s = State(b, None, 'init')
   >>> s
   142358607-init-0
   >>> dfs = DFSearcher(-1)
   >>> dfs.add_state(s)
   >>> dfs.next_state()     # remove the initial state
   142358607-init-0
   >>> succ = s.generate_successors()
   >>> succ
   [142308657-up-1, 142358067-left-1, 142358670-right-1]
   >>> dfs.add_states(succ)
   >>> dfs.next_state()   # the last one added, not the first!
   142358670-right-1
   >>> dfs.next_state()
   142358067-left-1
   

3. In eight_puzzle.py, there is a helper function called create_searcher that is used to create the appropriate type of searcher object. Modify this helper function so that it will be able to create objects that perform BFS and DFS. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'BFS' or 'DFS'. Once you do so, you should be able to use the eight_puzzle driver function to test your BFSearcher and DFSearcher classes.

   Breadth-first search should quickly solve the following puzzle:

   >>> eight_puzzle('142358607', 'BFS', -1)
   BFS: 0.006 seconds, 56 states
   Found a solution requiring 5 moves.
   Show the moves (y/n)?
   

   You may get a different time than we did, but the rest of the results should be the same. As discussed in class, BFS finds an optimal solution for eight-puzzle problems, so 5 moves is the fewest possible moves for this particular initial state.

   Depth-first search, on the other hand, ends up going deep in the search tree before it finds a goal state:

   >>> eight_puzzle('142358607', 'DFS', -1)
   DFS: 10.85 seconds, 3100 states.
   Found a solution requiring 3033 moves.
   Show the moves (y/n)?
   

   Important: In cases like this one in which the solution has an extremely large number of moves, trying to show the moves is likely to cause an error. That’s because our print_moves_to method uses recursion, and the number of recursive calls is equal to the number of moves in the solution. Each recursive call adds a new stack frame to the top of the memory stack, and we can end up overflowing the stack when we make that many recursive calls.

   To get a solution from DFS with fewer moves, we can impose a depth limit by passing it in as the third argument to the eight_puzzle function. For example:

   >>> eight_puzzle('142358607', 'DFS', 25)
   DFS: 6.945 seconds, 52806 states
   Found a solution requiring 23 moves.
   Show the moves (y/n)?
   

   Using a depth limit of 25 keeps DFS from going too far down a bad path, but the resulting solution requires 23 moves, which is still far from optimal!

Informed state-space search: Greedy and A*

4. In searcher.py, define a class called GreedySearcher for searcher objects that perform greedy search. As discussed in class, greedy search is an informed search algorithms that uses a heuristic function to estimate the remaining cost needed to get from a given state to the goal state (for the Eight Puzzle, this is just an estimate of how many additional moves are needed). Greedy Search uses this heuristic function to assign a priority to each state, and it selects the next state based on those priorities.

   Once again, this class should be a subclass of the Searcher class that you implemented in [Part III][partIII], and you should take full advantage of inheritance. However, the changes required in this class will be more substantial that the ones in BFSearcher and DFSearcher. Among other things, GreedySearcher objects will have a new attribute called heuristic that will allow you to choose among different heuristic functions, and they will also have a new method for computing the priority of a state.

   Here are the necessary steps:

   1. Make sure that your class header specifies that GreedySearcher inherits from Searcher.

   2. Define the constructor for the GreedySearches class. Copy the following code into the GreedySearcher class:

          def __init__(self, depth_limit, heuristic):
          """ constructor for a GreedySearcher object
              inputs:
               * depth_limit - the depth limit of the searcher
               * heuristic - a reference to the function that should be used 
               when computing the priority of a state
          """
          # add code that calls the superclass constructor
      
          self.heuristic = heuristic
      

      Two things worth noting:

      • GreedySearcher objects have an extra attribute called heuristic (and an associated extra input to their constructor). This attribute stores a reference to
        which heuristic function the GreedySearcher should use. We’re not currently using this attribute in our priority method, but ultimately the method will use this attribute to choose between multiple different heuristic functions for estimating a State‘s remaining cost. If needed, you should review the powerpoint notes about this on Blackboard.

      • A GreedySearcher object’s states attribute is not just a list of states. Rather, it is a list of lists, where each sublist is a [priority, state] pair. This will allow a GreedySearcher to choose its next state based on the priorities of the states.

      Example:

      >>> b = Board('142358607')       
      >>> s = State(b, None, 'init')
      >>> g = GreedySearcher(-1, h1)  # no depth limit, basic heuristic
      

      If you don’t see a priority value of -5, check your priority method for possible problems.

   3. Write a method priority(self, state) that takes a State object called state, and that computes and returns the priority of that state. For now, the method should compute the priority as follows:

      priority = -1 * num_misplaced_tiles
      

      where num_misplaced_tiles is the number of misplaced tiles in the Board object associated with state. Take advantage of the appropriate Board method to determine this value.

   4. Write a method add_state(self, state) that overrides (i.e., replaces) the add_state method that is inherited from Searcher. Rather than simply adding the specified state to the list of untested states, the method should add a sublist that is a [priority, state] pair, where priority is the priority of state, as determined by calling the priority method.

      Examples:

      >>> b = Board('142358607')       
      >>> s = State(b, None, 'init')
      >>> g = GreedySearcher(-1, h1)
      >>> g.add_state(s)
      >>> g.states
      [[-5, 142358607-init-0]]
      >>> succ = s.generate_successors()
      >>> g.add_state(succ[0])
      >>> g.states
      [[-5, 142358607-init-0], [-5, 142308657-up-1]]
      >>> g.add_state(succ[1])
      >>> g.states
      [[-5, 142358607-init-0], [-5, 142308657-up-1], [-6, 142358067-left-1]]
      

   5. Write a method next_state(self) that overrides (i.e., replaces) the next_state method that is inherited from Searcher. This version of next_state should choose one of the states with the highest priority.

      Hints:

      • You can use max to find the sublist with the highest priority. If multiple sublists are tied for the highest priority, max will choose one of them.

      • You should remove the selected sublist from states, and you should return only the state component of the sublist – not the entire sublist.

      Examples:

      >>> b = Board('142358607')       
      >>> s = State(b, None, 'init')
      >>> g = GreedySearcher(-1, h1)  # no depth limit, basic heuristic
      >>> g.add_state(s)
      >>> succ = s.generate_successors()
      >>> g.add_state(succ[1])
      >>> g.states
      [[-5, 142358607-init-0], [-6, 142358067-left-1]]
      >>> g.next_state()    # -5 is the higher priority
      142358607-init-0
      >>> g.states
      [[-6, 142358067-left-1]]
      

5. In searcher.py, define a class called AStarSearcher for searcher objects that perform A* search. Like greedy search, A* is an informed search algorithm that assigns a priority to each state based on a heuristic function, and that selects the next state based on those priorities. However, when A* assigns a priority to a state, it also takes into account the cost that has already been expended to get to that state (i.e. the number of moves to that state). More specifically, the priority of a state is computed as follows:

   priority = -1 * (heuristic + num_moves)
   

   where heuristic is the value that the selected heuristic function assigns to the state, and num_moves is the number of moves that it took to get to that state from the initial state.

   Once again, you should take full advantage of inheritance. However, we’re leaving it up to you decide which class to inherit from and how much new, non-inherited code is needed!

   Here’s one thing you need to know: When constructing an AStarSearcher object, you will need to specify two inputs: (1) function that specifies which heuristic function should be used, and (2) an integer for the depth limit. See below for an example of constructing one.

   Examples:

   >>> b = Board('142358607')       
   >>> s = State(b, None, 'init')
   >>> a = AStarSearcher(-1, h1)  # no depth limit, basic heuristic
   >>> a.add_state(s)
   >>> a.states          # init state has same priority as in greedy
   [[-5, 142358607-init-0]]
   >>> succ = s.generate_successors()
   >>> a.add_state(succ[1])
   >>> a.states         # succ[1] has a priority of -1*(6 + 1) = -7
   [[-5, 142358607-init-0], [-7, 142358067-left-1]]
   >>> a.next_state()   # -5 is the higher priority
   142358607-init-0
   >>> a.states
   [[-7, 142358067-left-1]]
   

6. Modify the create_searcher helper function in eight_puzzle.py so that it will be able to create GreedySearcher and AStarSearcher objects. To do so, simply uncomment the lines that handle cases in which the algorithm input is 'Greedy' or 'A*'.

   After you do so, try using the eight_puzzle driver function to see how the informed search algorithms perform on various puzzles. Here are some digit strings for puzzles that you might want to try, along with the number of moves in their optimal solutions:

   • '142358607' - 5 moves
   • '031642785' - 8 moves
   • '341682075' - 10 moves
   • '631074852' - 15 moves
   • '763401852' - 18 moves
   • '145803627' - 20 moves

   A* should obtain optimal solutions; Greedy Search may or may not.

   If a given algorithm ends up taking longer than you can afford to wait, you can stop it by using Ctrl-C from the keyboard.

Part V: Compare algorithms, and try to speed things up!

In this last part of the project, you will write code to facilitate the comparison of the different state-space search algorithms, and you will also attempt to speed things up so that your code can more easily solve puzzles that require many moves.

Your tasks

1. In eight_puzzle.py, write a function named process_file(filename, algorithm, depth_limit = -1, heuristic = None). It should take the following four inputs:

   • a string filename specifying the name of a text file in which each line is a digit string for an eight puzzle. For example, here is a sample file containing 10 digit strings, each of which represents an eight puzzle that can be solved in 10 moves: 10_moves.txt

   • a string algorithm that specifies which state-space search algorithm should be used to solve the puzzles ('random', 'BFS', 'DFS', 'Greedy', or 'A*')

   • an integer depth_limit that can be used to specify an optional parameter for the depth limit

   • an optional parameter heuristic, which will be used to pass in a reference to the heuristic function to use.

   To make the third and fourth parameters optional, you should use the following function header:

   def process_file(filename, algorithm, depth_limit=-1, heuristic=None):
       """ doctring goes here
       """
   

   Note that this header specifies a default value of -1 for the input depth_limit, which is why this input is optional. If we leave it out (by only specifying two inputs when we call the function), Python will give depth_limit its default value of -1. If we specify a value for depth_limit when we call the function, the specified value will be used instead of -1.

   This function header also specifies a default value of None for the heuristic, which is why this input is optional. If we leave it out when we call the function, we will use the default value of None. If we specify a heuristic in the function call, we will use that heuristic function.

   Your function should open the file with the specified filename for reading, and it should use a loop to process the file one line at a time.

   For each line of the file, the function should:

   • obtain the digit string on that line (stripping off the newline at the end of the line)

   • take the steps needed to solve the eight puzzle for that digit string using the algorithm specified by the second input to the function

   • report the number of moves in the solution, and the number of states tested during the search for a solution

   In addition, the function should perform the cumulative computations needed to report the following summary statistics after processing the entire file:

   • number of puzzles solved
   • average number of moves in the solutions
   • average number of states tested

   For example:

   >>> process_file('10_moves.txt', 'BFS')
   125637084: 10 moves, 661 states tested
   432601785: 10 moves, 1172 states tested
   025318467: 10 moves, 534 states tested
   134602785: 10 moves, 728 states tested
   341762085: 10 moves, 578 states tested
   125608437: 10 moves, 827 states tested
   540132678: 10 moves, 822 states tested
   174382650: 10 moves, 692 states tested
   154328067: 10 moves, 801 states tested
   245108367: 10 moves, 659 states tested
   
   solved 10 puzzles
   averages: 10.0 moves, 747.4 states tested
   

   (In this case, because BFS finds optimal solutions, every solution has the same number of moves, but for other algorithms this won’t necessarily be the case.)

   Notes/hints:

   • You can model your code for solving a given puzzle on the code that we’ve given you in the eight_puzzle driver function. In particular, you can emulate the way that this function:

     • creates Board and State objects for the initial state
     • calls the create_searcher helper function to create the necessary type of searcher object, and handles the possible return value of None from that function

   • When calling the searcher object’s find_solution method, you should do so as follows:

     soln = None
     try:
         soln = searcher.find_solution(s)
     except KeyboardInterrupt:
         print('search terminated, ', end='')
     

     Making the call to find_solution(s) in this way will allow you to terminate a search that goes on too long by using Ctrl-C. In such cases, soln will end up with a value of None (meaning that no solution was found), and you should make sure to properly handle such cases.

   • You should not use a timer in this function.

   • This function should not return a value.

   Testing your function:

   • If you haven’t already done so, download the 10_moves.txt file, putting it in the same folder as the rest of your files for the project.

   • Try to reproduce the results for BFS shown above.

   • Try applying Greedy Search to the same file. You may find that it takes Greedy a very long time to solve some of the puzzles, at least when using the num-misplaced-tiles heuristic. If this happens, use Ctrl-C as needed to terminate the problematic searches. When we processed 10_moves.txt using our implementation of Greedy, we ended up using Ctrl-C to terminate two of the searches:

     >>> process_file('10_moves.txt', 'Greedy', -1, h1)
     125637084: 204 moves, 658 states tested
     432601785: 12 moves, 13 states tested
     025318467: search terminated, no solution
     134602785: 78 moves, 221 states tested
     341762085: 26 moves, 339 states tested
     125608437: 162 moves, 560 states tested
     540132678: 68 moves, 749 states tested
     174382650: search terminated, no solution
     154328067: 10 moves, 16 states tested
     245108367: 48 moves, 49 states tested
     
     solved 8 puzzles
     averages: 76.0 moves, 325.625 states tested
     

   • It’s also possible for none of the puzzles to have a solution, and you should handle that situation appropriately. For example, this can happen if you impose a depth limit that is too small:

     >>> process_file('10_moves.txt', 'DFS', 5)    # depth limit of 5
     125637084: no solution
     432601785: no solution
     025318467: no solution
     134602785: no solution
     341762085: no solution
     125608437: no solution
     540132678: no solution
     174382650: no solution
     154328067: no solution
     245108367: no solution
     
     solved 0 puzzles
     

     Note that you can’t compute any averages in this case, so you shouldn’t print the averages line in the results.

2. Create a plain-text file named results.txt, and put your name and email (and those of your partner, if any) at the top of the file.

3. Conduct an initial set of experiments in which you try all of the algorithms on the puzzles in the following files:

   • 5_moves.txt - puzzles that can be solved in 5 moves
   • 10_moves.txt - puzzles that can be solved in 10 moves
   • 15_moves.txt - puzzles that can be solved in 15 moves

   More specifically, you should run the following algorithms on each file:

   • random
   • BFS
   • DFS with a depth limit of 20
   • DFS with a depth limit of 50
   • Greedy (using the default, num-misplaced-tiles heuristic)
   • A* (using the same heuristic)

   Note that it may be necessary to use Ctrl-C to terminate searches that take too much time. You might want to pick a given amount of time (e.g., 30 seconds or 1 minute), and use Ctrl-C to terminate any search that doesn’t complete in that time.

   In your results.txt file, create three tables that summarize the results of these initial experiments. Use a separate table for each file’s results. For example, the results for 5_moves.txt should be put into a table that looks like this:

   puzzles with 5-move optimal solutions
   -------------------------------------
   algorithm              num. solved    avg. moves    avg. states tested
   ----------------------------------------------------------------------
   random
   BFS
   DFS (depth limit 20)
   DFS (depth limit 50)
   Greedy Search
   A*
   

   Below these tables, write a short reflection (one or two paragraphs) in which you summarize the key points that are illustrated by the results. For example, you might discuss whether the algorithms produce reliably optimal results, and how much work they do in finding a solution. There’s no one correct reflection; we just want to see that you have reflected intelligently on the results and drawn some conclusions.

4. Even informed search algorithms like Greedy Search and A* can be slow on problems that require a large number of moves. This is especially true if the heuristic function used by the algorithm doesn’t do a good enough job of estimating the remaining cost to the goal.

   Our default heuristic–which uses the number of misplaced tiles as the estimate of the remaining cost–is one example of a less than ideal heuristic. For example, consider the following two puzzles:

   

   Both of them have 4 misplaced tiles (the ones displayed in red), but the puzzle on the left can be solved in 4 moves, whereas the puzzle on the right requires 24 moves! Clearly, it would be better if our heuristic could do a better job of distinguishing between these two puzzles.

   Come up with at least one alternate heuristic, and use it in your GreedySearcher or AStarSearcher objects.

   To do so, you should take the following steps:

   1. Define a function (e.g., h1(state) or h2(state)) in your searcher.py file. This function will take a State object as a parameter, and return a heuristic value (i.e., a number).

   2. To use this function as your heuristic, you will pass it into the constructor for GreedySearcher or AStarSearcher objects. For example:

      >>> g = GreedySearcher(-1, h1) # no depth limit, basic heuristic
      

      where h1 is the heuristic function to use, and -1 is the depth limit

      When using the eight_puzzle driver function or the process_file function that you wrote earlier, you should specify the heuristic number as the third input. For example:

      >>> process_file('15_moves.txt', 'A*', -1, h1)  # no depth limit, basic heuristic
      

   3. Update the code in your informed searcher classes so that the process of assigning priorities to states uses your new heuristic.

      For example, you will need to update the body of the priority method in GreedySearcher to look something like this:

      def priority(self, state):
      
          # use my new heuristic
          h = self.heuristic(state)
      
          # possibly other code here
      

   You are welcome to design more than one new heuristic function, although only one is required. Give each heuristic its own integer so that you can choose between them.

   When testing and refining your heuristic(s), you can use the files that we provided above, as well as the following files:

   • 18_moves.txt - puzzles that can be solved in 18 moves
   • 21_moves.txt - puzzles that can be solved in 21 moves
   • 24_moves.txt - puzzles that can be solved in 24 moves
   • 27_moves.txt - puzzles that can be solved in 27 moves

   Compare the performance of Greedy and A* using the default heuristic to their performance using your new heuristic(s). Keep revising your heuristic(s) as needed until you are satisfied. Ideally, you should see the following when using your new heuristic(s):

   • Both algorithms are able to solve puzzles more quickly – testing fewer states on average and requiring fewer searches to be terminated.
   • Greedy Search is able to find solutions requiring fewer moves.
   • A* continues to find optimal solutions. (If it starts finding solutions with more than the optimal number of moves, that probably means that your heuristic is overestimating the remaining cost for at least some states.)

5. Although you are welcome to keep more than one new heuristic function, we will ultimately test only one of them. Please adjust your code as needed so that the heuristic that you want us to test is identified using the name h2. Also, please make sure that we will still be able to test the default, num-misplaced-tiles heuristic if we specify a value of h1 for the heuristic.

   In your results.txt file, briefly describe how your best new heuristic works:

   heuristic 1
   -----------
   This heuristic ...
   

   If your code includes other alternate heuristics, you are welcome to describe them as well, although doing so is not required.

6. Conduct a second set of experiments in which you try both your new heuristic(s) and the default heuristic on the puzzles in the four new files provided above (the ones that require 18, 21, 24, and 27 moves).

   In your results.txt file, create four tables that summarize the results of these experiments. Use a separate table for each file’s results. For example, the results for 18_moves.txt should be put into a table that looks like this:

   puzzles with 18-move optimal solutions
   --------------------------------------
   algorithm              num. solved    avg. moves    avg. states tested
   ----------------------------------------------------------------------
   Greedy (heuristic h1)
   Greedy (heuristic h2)
   # Greedy with any other heuristics
   
   A* (heuristic h1)
   A* (heuristic h2)
   # Greedy with any other heuristics
   

   Below these tables, write a short reflection (one or two paragraphs) in which you summarize the key points that are illustrated by the results. Here again, there is no one correct reflection; we just want to see that you have reflected intelligently on the results and drawn some conclusions.

Submitting Your Work

You should use Gradesope to submit the following files:

• your final board.py file
• your final state.py file
• your final searcher.py file
• your eight_puzzle.py file
• your results.txt file containing the results of your experiments