Assignment 9: Monte Carlo Simulation and Pricing Exotic Options

Discussion on Thursday 3/21/2024
Workshop in class on Tuesday 3/26/2024
Submission due by 9:00 p.m. on Wednesday 3/27/2024.

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

For each problem in this problem set, we will be writing or evaluating some Python code. You are encouraged to use the Spyder IDE which will be discussed/presented in class, but you are welcome to use another IDE if you choose.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Objective and Overview

Objective: Learn to use the numpy numerical programming toolkit and Monte Carlo simulation. Additional practice with object-oriented programming, class definintions, inheritance, and polymorphism.

Overview: In this assignment, you will implement some classes to simulate stock returns and price movements (task 1) to assist with pricing path-dependent options (task 2). In the first task, you will implement a base class to encapsulate the fundamental data members and common calculations used to simulate stock returns using Monte Carlo simulation. In the second task, you will create subclasses to implement several option pricing algorithms.

Task 1: Simulating Stock Returns

40 points; individual-only

Monte Carlo Simulation is a mathematical technique in which we use data generated at random to help understand what might occur in some real scenario. It is used in a wide variety of domains to simulate outcomes that follow some known (or assumed) probability distribution. In finance, Monte Carlo methods are used to simulate stock returns, and can be instrumental in pricing some assets for which an analytical pricing formula does not exist.

In this task, you will write a definition for the class MCStockSimulator, which encapsulates the data and methods required to simulate stock returns and values. This class will serve as a base class for option pricing classes (in part 2).

Do this entire task in a file called a9task1.py.

1. Create the __init__ and __repr__ methods for the class MCStockSimulator, such that you can create and print out an object like this:

   Example:

   >>> # initial stock price = $100; 1 year time frame
   >>> # expected rate of return = 10%; standard deviation = 30%; 
   >>> # 250 discrete time periods per year
   >>> sim = MCStockSimulator(100, 1, 0.1, 0.3, 250)
   >>> print(sim)
   MCStockSimulator (s=$100.00, t=1.00 (years), mu=0.10, sigma=0.30, nper_per_year=250)
   

   The data required include:
   s (the current stock price in dollars),
   t (the option maturity time in years),
   mu (the annualized rate of return on this stock),
   sigma (the annualized standard deviation of returns),
   nper_per_year (the number of discrete time periods per year)
   

2. Write a method generate_simulated_stock_returns(self) on your class MCStockSimulator, which will generate and return a np.array (numpy array) containing a sequence of simulated stock returns over the time period t.

   For example, here is a MCStockSimulator for a 1-year time horizon, with 2 discrete periods per year:

   >>> sim = MCStockSimulator(100, 1, 0.10, 0.30, 2)
   >>> sim.generate_simulated_stock_returns()
   array([ 0.19029749, -0.07209056])
   

   Here is a MCStockSimulator for a 1-year time horizon, with 4 discrete periods per year:

   >>> sim = MCStockSimulator(100, 1, 0.10, 0.30, 4)
   >>> sim.generate_simulated_stock_returns()
   array([ 0.09513401, -0.05576265, -0.05610946,  0.05004434])
   

   Here is a MCStockSimulator for a 0.5-year time horizon, with 2 discrete periods per year:

   >>> sim = MCStockSimulator(100, 0.5, 0.10, 0.30, 2)
   >>> sim.generate_simulated_stock_returns()
   array([0.09416193])
   

   Notice that in 0.5 years, it only generates one simulated return (i.e, 2 periods per for 0.5 years is one periodic return).

   Finally, here is a 5-year simulation with 250 discrete time periods per year (i.e., 250 stock market trading days per year).

   >>> sim = MCStockSimulator(100, 5, 0.10, 0.30, 250)
   >>> returns = sim.generate_simulated_stock_returns()
   >>> len(returns)
   1250
   

   Algorithm to generate simulated stock returns

   One method for creating simulated stock returns is to assume that future returns will follow the same probability distribution as historical returns. Let’s assume that stock returns have historically been approximately normally distributed with a mean mu and standard deviation sigma. We can simiulate the annual rate of return as:

   

   where Z is a randomly-drawn number from the standard normal distribution. You can draw such a number using the function np.random.normal().

   To find a simulated rate of return for an arbitrary discrete time period dt, we can use this formula: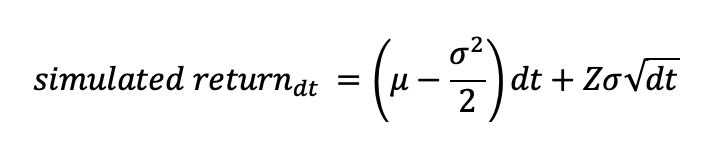

   

   Where mu is the mean historical annual rate of return on the stock, and sigma is the historical annual standard deviation on the stock.

   Notes/Hints:

   • Each run of generate_simulated_stock_returns() will return a new, independent sequence of simulated stock returns. You should not expect to get the same result twice!

   • The returns in this sequence represent a simluated run through t years, with nper_per_year discrete steps per year. It might be helpful to create a variable dt = 1/nper_per_year to represent the length of each discrete time period.

3. Write a method generate_simulated_stock_values(self) on your class MCStockOption, which will generate and return a np.array (numpy array) containing a sequence of stock values, corresponding to a random sequence of stock return. There are t * nper_per_year discrete time periods, where t is the length of the simulation.

   We create a sequence of simulated stock values as follows. The stock value (i.e., price) at each time interval (i) is based on the stock value at the previous time interval (i-1), and the rate of return earned in that time interval (i-1):

   

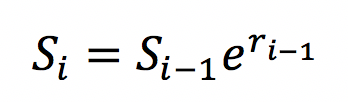
   We refer to this sequence of prices as the price path of the stock, i.e., the price of the stock at each discrete time period from time 0 until time T.

   For example, here is a 1-year simulation with the stock value in each of 4 discrete time periods:

   >>> sim = MCStockSimulator(100, 1, 0.10, 0.30, 4)
   >>> sim.generate_simulated_stock_values()
   array([100.        ,  88.47469462,  72.57503698,  91.67212336,      89.84643091])
   

   For example, here is a 2-year simulation with the stock value in each of 24 discrete time periods:

   >>> sim = MCStockSimulator(100, 2, 0.10, 0.30, 24)
   >>> sim.generate_simulated_stock_values()
   array([100.        , 100.64476047,  92.44751783,  89.62159243,
   90.43944749,  84.47777912,  86.64219253,  83.70486646,
   82.41160488,  79.61249678,  89.37948238,  89.51053126,
   84.08907477,  88.63605364,  82.43987728,  83.69265041,
   74.39866774,  68.74439796,  69.7377763 ,  73.13122862,
   74.07227217,  73.71829114,  72.5375137 ,  66.41048256,
   63.69240377,  62.06292089,  66.36538706,  67.93215897,
   61.11989899,  62.48803934,  61.1717485 ,  58.82249127,
   61.20771985,  65.34628289,  69.33995232,  66.01761177,
   64.92793123,  66.41050359,  70.66049108,  68.77463151,
   68.15314952,  63.83490455,  59.46211602,  62.63898906,
   68.21960455,  68.07526597,  72.55603797,  74.35095079,
   71.63492769])
   

   Notes/Hints:

   • You should re-use your generate_simulated_stock_returns() to obtain the sequence of returns for the simulation. Next, you will use the returns to create the stock values for the simulation, beginning with the initial stock price s.

   • Notice that in the first example, we created a simulation with 4 periods. The resulting np.array contained 5 values: the initial price at time 0, plus the 4 discrete steps.

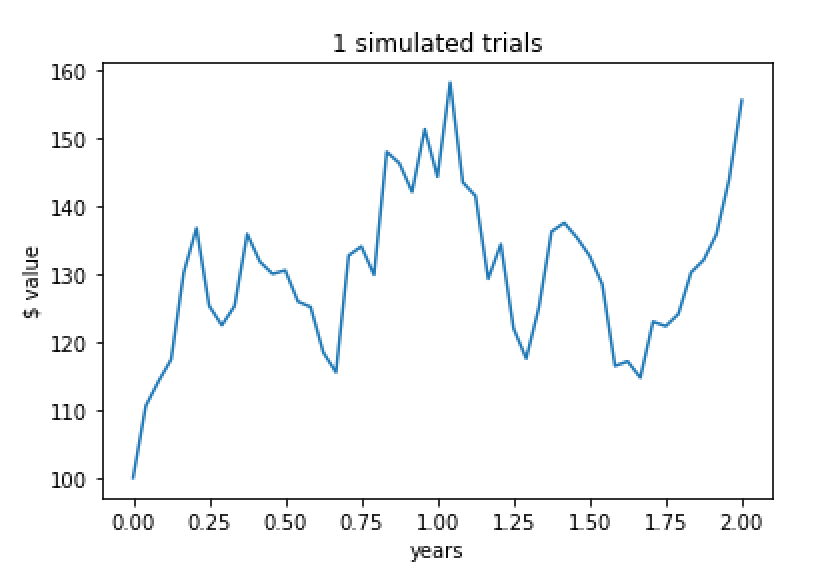
4. Write the method plot_simulated_stock_values(self, num_trials = 1), that will generate a plot of of num_trials series of simulated stock returns. num_trials is an optional parameter; if it is not supplied, the default value of 1 will be used.

   For example, consider this sequence of operations:

   >>> sim = MCStockSimulator(100, 2, 0.10, 0.30, 24)
   >>> sim.plot_simulated_stock_values()
   

   which generates this plot:

   

   We can also generate multiple simulations on a single plot, by passing in the parameter num_trials. For example:

   >>> sim = MCStockSimulator(100, 2, 0.10, 0.30, 250)
   >>> sim.plot_simulated_stock_values(5)
   

   which generates this plot:

   

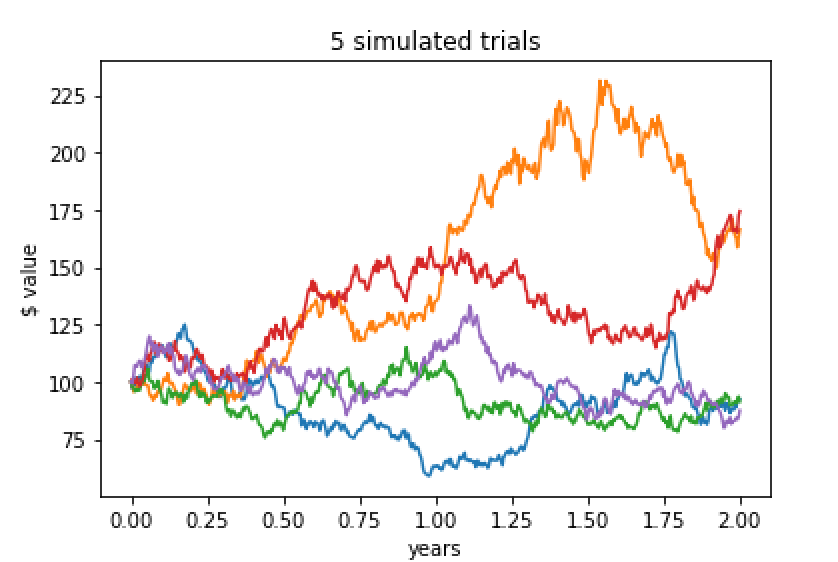
   In the above plot, each line represents one simulated price-path over a period of 5 years, with 250 discrete time periods per year.

   Notes/Hints:

   • Each run of plot_simulated_stock_values() will return a new, independent plot of simulated stock values. You should not expect to get the same result twice!

   • You should re-use your generate_simulated_stock_values() method to obtain a sequence of stock values for each of num_trials trials.

   • Use the matplotlib library to generate the plots.

   • The matplotlib plot method accepts parameters that are of type numpy.array.
     We can pass in a 2-dimensional numpy.array of y-values, where each y-value corresponds to one x-value.

   • The matplotlib library will automatically assign colors to each plot line, so you don’t need to.

Task 2: Pricing Path-Dependent Options

40 points; individual-only

The Black-Scholes method provides the most efficient way to value standard options, such as the European call or put options. However, there exist many types of exotic options for which the payoff depends on the price path of the underlying assets, and thus require a technique to simulate the path of a stock price (or other underlying asset) through time.

We will use object-oriented techniques to implement a hierarchy of option classes, extensible to many different kinds of options with similar fundamental characteristics such as the underlying stock’s mean rate of return and standard deviation of returns, but with different payoff algorithms (e.g., European, average price, or no-regret options).

Do this task in a file called a9task2.py. You will need to import the class MCStockSimulator from your a9task1.py file, as well as importing the numpy module, i.e.,

    from a9task1 import MCStockSimulator
    import numpy as np

1. Write a class definition for the class MCStockOption, which inherits from MCStockSimulator. This class will encapsulate the idea of a Monte Carlo stock option, and will contain some additional data members( that are not part of class MCStockSimulator and are required to run stock-price simulations and calculate the option’s payoff. However, this class will not be a concrete option type, and thus will not implement the option’s value algorithm, which differs for each concrete option type.

   a. Write an __init__ method that takes the following parameters:
   s, which is the initial stock price
   x, which is the option’s exercise price
   t, which is the time to maturity (in years) for the option
   r, which is the annual risk-free rate of return
   sigma, which is the annual standard deviation of returns on the underlying stock
   nper_per_year, which is the number of discrete time periods per year with which to evaluate the option, and
   num_trials, which is the number of trials to run when calculating the value of this option
   

   The constructor for MCStockOption will need to explicitly call the super class’s constructor to initialize the data attributes of the super class. Only two new data attributes are created in this subclass (x, and num_trials); the value of r will be passed into the super class in place of the parameter mu.

   b. Write a __repr__ method to create a nicely formatted printout of the MCStockOption object, which will be useful for debugging your work.

   >>> option = MCStockOption(90, 100, 1.0, 0.1, 0.3, 250, 10)
   >>> print(option)
   MCStockOption (s=$90.00, x=$100.00, t=1.00 (years), r=0.10, sigma=0.30, nper_per_year=250, num_trials=10)
   

2. Add the following methods to your class MCStockOption:

   a. the method value(self), which will return the value of the option. This method cannot be concretely implemented in this base class, but will be overridden in each subclass (see below). For now, the method should print out an informational message and return 0.

   Example:

   >>> option = MCStockOption(90, 100, 1.0, 0.1, 0.3, 250, 10)
   >>> option.value()
   Base class MCStockOption has no concrete implementation of .value(). # print statement
   0 # this is the return value
   

   b. the method stderr(self), which will return the standard error of this option’s value. The standard error is calculated as stdev / sqrt(num_trials), where stdev is the standard deviation of the values obtained from many trials.

   The standard error can only be calculated after running some trials, and as such it cannot be calculated until we implement the value(self) method in the concrete subclasses (explained below). For now, you should use the following method definition in class MCStockOption:

   def stderr(self):
       if 'stdev' in dir(self):
           return self.stdev / math.sqrt(self.ntrials)
   return 0
   

3. Write a class definition for the class MCEuroCallOption which inherits from the base class MCStockOption.

   For example:

   >>> call = MCEuroCallOption(90, 100, 1, 0.1, 0.3, 100, 1000)
   >>> print(call)
   MCEuroCallOption (s=$90.00, x=$100.00, t=1.00 (years), r=0.10, sigma=0.30, nper_per_year=100, num_trials=1000)
   >>> call.value()
   11.13033565434845 ## your value WILL be different but should be relatively close
   

   Calculating the option value:

   The value of the European call option is calculated by:

   

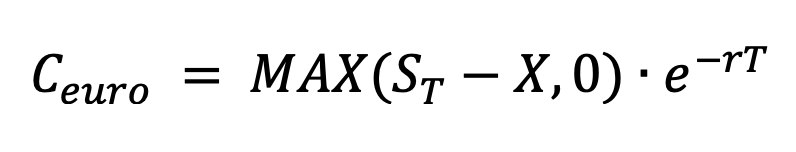
   where S_t is the value of the underlying stock in the last discrete time period.

   Note that each time your execute the .value() method, you will get a different result to to the nature of the random trials:

   >>> call.value()
   10.325308111873307
   >>> call.value()
   10.343625341278162
   >>> call.value()
   10.791846055464116
   

   The standard error of the option’s value describes how good or bad this estimate is. In this case for a call option value calculated with 1000 random trials, the standard error is quite large:

   >>> call.stderr()
   0.6258359263169805 # about $0.63
   

   We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

   >>> call = MCEuroCallOption(90, 100, 1, 0.1, 0.3, 100, 1000)
   >>> print(call)
   MCEuroCallOption (s=$90.00, x=$100.00, t=1.00 (years), r=0.10, sigma=0.30, nper_per_year=100, num_trials=1000)
   >>> call.value()
   10.649488858877 
   >>> call.stderr()
   0.6512665650642401 # large! about $0.65
   >>> # change ntrials from 1,000 to 100,000
   >>> call.num_trials = 100000
   >>> call.value() # note: this took about 20 seconds to run on my computer; if it takes several minutes, something is wrong!
   10.3951924480017
   >>> call.stderr()
   0.058644018813245935 # better; about $0.06
   

   The value of this option given by Black-Scholes is:

   >>> bs_call = BSEuroCallOption(90, 100, 1.0, 0.3, 0.10)
   >>> bs_call.value()
   10.51985812604488  # the MC option value was pretty close
   

   We can obtain a closer estimate by further increasing the number of trials, i.e.,

   >>> # change ntrials from 1,000 to 1,000,000
   >>> call.num_trials = 1000000
   >>> call.value() # this calculation took about 2 minutes on my computer.
   10.537749946259456
   >>> call.stderr()
   0.01878190454494842 # small! about $0.02
   

   Notice that using Monte Carlo simulation to calculate the value is very inefficient for European call/put options. However, pricing European call options via our Monte Carlo simulation is a good way to check that our simulation is working correctly, i.e., we can check the value obtained for these options against the values from Black-Scholes.

   Here is one more example against which you can test your work:

   >>> bs_call = BSEuroCallOption(40, 40, 0.25, 0.3, 0.08)
   >>> bs_call.value()
   2.7847366578216608
   >>> call = MCEuroCallOption(40, 40, 0.25, 0.08, 0.30, 100, 100000)
   >>> print(call)
   MCEuroCallOption (s=$40.00, x=$40.00, t=0.25 (years), r=0.08, sigma=0.30, nper_per_year=100, num_trials=100000)
   >>> call.value()
   2.7940360768116648
   >>> call.stderr()
   0.012941916180648372
   

4. Write a class definition for the class MCEuroPutOption which inherits from the base class MCStockOption.

   For example:

   >>> put = MCEuroPutOption(100, 100, 1.0, 0.1, 0.3, 100, 1000)
   >>> print(put)
   MCEuroPutOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.10, sigma=0.30, nper_per_year=100, num_trials=1000)
   >>> put.value()
   7.180043862237398
   

   Calculating the option value:

   The value of the European put option is calculated by:

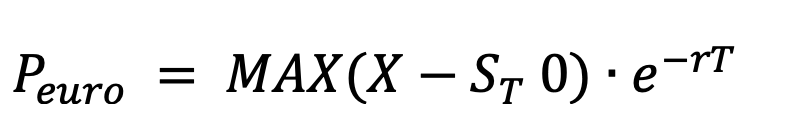
   where S_t is the value of the underlying stock in the last discrete time period.

   Note that each time your execute the .value() method, you will get a different result to to the nature of the random trials:

   >>> put.value()
   7.606982016445182
   >>> put.value()
   7.733699836474863
   >>> put.value()
   6.962009593006104
   >>> put.value()
   7.228000254327266
   

   The standard error of the option’s value describes how good or bad this estimate is. In this case for a call option value calculated with 1000 random trials, the standard error is quite large:

   >>> put.stderr()
   0.35918784509458573 # about $0.36
   

   We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

   >>> put = MCEuroPutOption(100, 100, 1.0, 0.1, 0.3, 100, 100000)
   >>> print(put)
   MCEuroPutOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.10, sigma=0.30, nper_per_year=100, num_trials=100000)
   >>> put.value() ## this took about 17 seconds on my computer
   7.231449281956995
   >>> put.stderr()
   0.035643292753420035
   

   The value of this option given by Black-Scholes is:

   >>> bs_put = BSEuroPutOption(100, 100, 1.0, 0.3, 0.10)
   >>> bs_put.value()
   7.217875385982609
   

   Again, we note that Monte Carlo simulation to calculate the value is extremely inefficient for European call/put options. However, pricing European put options via our Monte Carlo simulation is a good way to check that our simulation is working correctly, i.e., we can check the values obtained for these options against the values we obtained using Black-Scholes.

5. Write a class definition for the class MCAsianCallOption which inherits from the base class MCStockOption. The Asian call option’s payoff the amount by which the average stock price exceeds the option’s exercise price during the option’s lifetime.

   (The “Asian” or average price option was developed by two British bankers, who just happened to be in Tokyo when “they developed the first commercially used pricing formula for options linked to the average price of crude oil.” - Wikipedia)

   Calculating the option value:

   The value of the Asian call option (in a single trial) is calculated by:

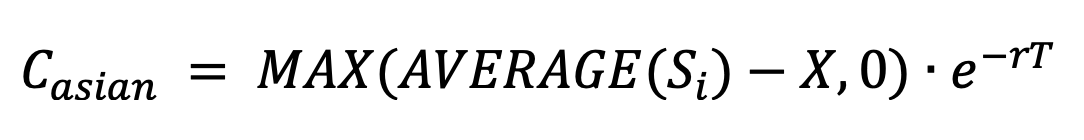
   where S is price-path of the of the underlying stock form now until time t.

   For example:

   >>> acall = MCAsianCallOption(100, 100, 1, 0.05, 0.30, 100, 1000)
   >>> print(acall)
   MCAsianCallOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.05, sigma=0.30, nper_per_year=100, num_trials=1000)
   >>> acall.value()
   8.241753807950401
   >>> acall.stderr()
   0.4059173818833795
   

   We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

       >>> # change ntrials to reduce the standard error:
       >>> acall.num_trials = 100000
       >>> acall.value()
       7.871304355528306
       >>> acall.stderr()
       0.037767487742632506
   

   There is no “exact” right answer, but we can increase the number of trials until the standard error is sufficiently small (e.g., maybe a standard error of $0.01 is “good enough”.)

   Here are some additional examples of Asian call options with different parameters:

   >>> acall = MCAsianCallOption(35, 30, 1.0, 0.05, 0.25, 100, 100000)
   >>> acall.value()
   5.821400468017319
   >>> acall.stderr()
   0.014707518162260144
   
   >>> acall = MCAsianCallOption(35, 40, 1.0, 0.05, 0.40, 100, 100000)
   >>> acall.value()
   1.735539867872192
   >>> acall.stderr()
   0.013270854536008715
   

6. Write a class definition for the class MCAsianPutOption which inherits from the base class MCStockOption. The Asian put option’s payoff the amount by which the option’s exercise price exceeds average stock price during the option’s lifetime.

   Calculating the option value:

   The value of the Asian put option (in a single trial) is calculated by:

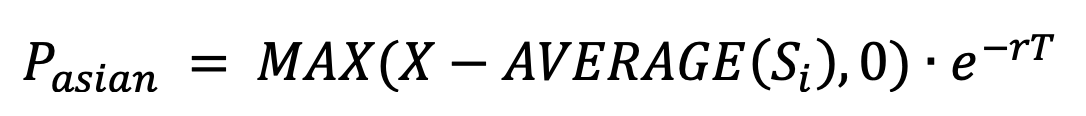
   where S is price-path of the of the underlying stock form now until time t.

   For example:

       >>> aput =  MCAsianPutOption(100, 100, 1, 0.05, 0.30, 100, 1000)
       >>> print(aput)
       MCAsianPutOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.05, sigma=0.30, nper_per_year=100, num_trials=1000)
       >>> aput.value()
       5.362777039902237
   >>> aput.stderr()
   0.24587955136040612
   

   We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

       >>> # change ntrials to reduce the standard error:
       >>> aput.num_trials = 100000
       >>> aput.value()
       5.529660046804241
       >>> aput.stderr()
       0.02514572453388165
   

   There is no “exact” right answer, but we can increase the number of trials until the standard error is sufficiently small (e.g., maybe a standard error of $0.01 is “good enough”.)

   Here are some additional examples of Asian put options with different parameters:

   >>> aput = MCAsianPutOption(35, 30, 1.0, 0.05, 0.25, 100, 100000)
   >>> aput.value()
   0.22206880461140133
   >>> aput.stderr()
   0.0025129290896946017
   
   >>> aput = MCAsianPutOption(35, 40, 1.0, 0.05, 0.40, 100, 100000)
   >>> aput.value()
   5.703977040389064
   >>> aput.stderr()
   0.01657552125060991
   

7. Write a class definition for the class MCLookbackCallOption which inherits from the base class MCStockOption. The look-back call option’s payoff is amount by which the maximum stock price exceeds the option’s exercise price during the option’s lifetime.

   Calculating the option value:

   The value of the look-back call option (in a single trial) is calculated by:

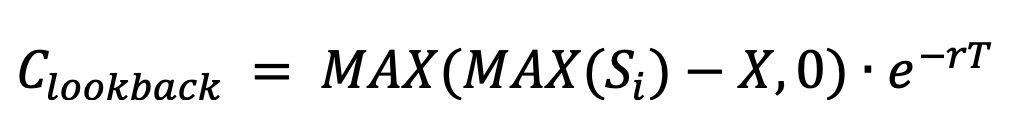
   where S is price-path of the of the underlying stock form now until time t.

   For example:

   >>> lcall = MCLookbackCallOption(100, 100, 1, 0.05, 0.30, 100, 1000)
   >>> print(lcall)
   MCLookbackCallOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.05, sigma=0.30, nper_per_year=100, num_trials=1000)
   >>> lcall.value()
   26.7818388316668
   >>> lcall.stderr()
   0.7745314888407241
   

   We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

       >>> # change ntrials to reduce the standard error:
       >>> lcall.num_trials = 100000
       >>> lcall.value()
       25.914021002647974
       >>> lcall.stderr()
       0.07633105161506483
   

   There is no “exact” right answer, but we can increase the number of trials until the standard error is sufficiently small (e.g., maybe a standard error of $0.01 is “good enough”.)

   Here are some additional examples of Lookback call options with different parameters:

   >>> lcall = MCLookbackCallOption(35, 30, 1.0, 0.05, 0.25, 100, 100000)
   >>> lcall.value()
   12.429571002010963
   >>> lcall.stderr()
   0.021738067919715248
   
   >>> lcall = MCLookbackCallOption(35, 40, 1.0, 0.05, 0.40, 100, 100000)
   >>> lcall.value()
   8.346534566163065
   >>> lcall.stderr()
   0.036387616621895914
   

8. Write a class definition for the class MCLookbackPutOption which inherits from the base class MCStockOption. The look-back put option’s payoff the amount by which the option’s exercise price exceeds the minimum stock price during the option’s lifetime.

   Calculating the option value:

   The value of the look-back call option (in a single trial) is calculated by:

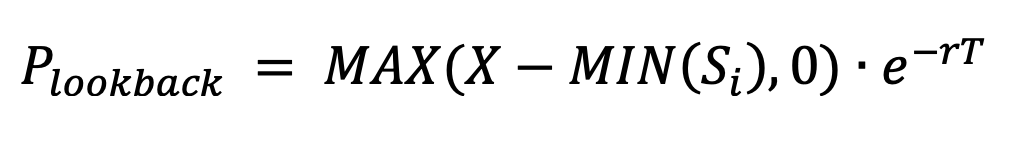
   where S is price-path of the of the underlying stock form now until time t.

For example:

    >>> lput = MCLookbackPutOption(100, 100, 1, 0.05, 0.30, 100, 1000)
    >>> print(lput)
    MCLookbackPutOption (s=$100.00, x=$100.00, t=1.00 (years), r=0.05, sigma=0.30, nper_per_year=100, num_trials=1000)
    >>> lput.value()
    17.08122050359968
>>> lput.stderr()
0.3931802045189811

We can obtain a better estimate of the option value (i.e., with lower standard error) by increasing the number of trials:

    >>> # change ntrials to reduce the standard error:
    >>> lput.num_trials = 100000
    >>> lput.value()
    17.515587516815582
    >>> lput.stderr()
    0.040406857611874555

There is no “exact” right answer, but we can increase the number of trials until the standard error is sufficiently small (e.g., maybe a standard error of $0.01 is “good enough”.)

Here are some additional examples of Lookback put options with different parameters:

>>> lput = MCLookbackPutOption(35, 30, 1.0, 0.05, 0.25, 100, 100000)
>>> lput.value()
1.737427849690544
>>> lput.stderr()
0.008359535335712818


>>> lput = MCLookbackPutOption(35, 40, 1.0, 0.05, 0.40, 100, 100000)
>>> lput.value()
1.7495373276783786
>>> lput.stderr()
0.013358607900741632

Submitting Your Work

20 points; will be assignmed by code review

Use the link to GradeScope (left) to submit your work.

Be sure to name your files correctly!

Under the heading for Assignment 9, attach these 3 required files: a9task1.py, a9task2.py and a9graphs.pdf

When you upload the files, the autograder will test your functions/programs.

*   Why does this happen? When the autograder imports your file, the `print` 
    statement(s) execute (at import time), which causes this error.

*   You can prevent this error by not having any `print` statements in the global scope.
    Instead, create an `if __name__ == '__main__':` section at the bottom of the file, and
    put any test cases/print statements in that controlled block. For example:

        if __name__ == '__main__':

            ## put test cases here:
            print('fv_lump_sum(0.05, 2, 100)', fv_lump_sum(0.05, 2, 100))

*   `print` statements inside of functions do not cause this problem.

Notes:

• You may resubmit multiple times, but only the last submission will be graded.