Assignment 3

Objective and Overview

Objective: The objective of this assignment is to practice working with lists, definite loops, the accumulator pattern, and file processing.

Overview: In this assignment, you will write several functions to process a list of numbers and generate the following descriptive statistics: mean, variance, standard deviation, covariance, correlation, and simple regression.

Next, you will write a program to process a data file containing stock price information, calculate stock returns, and generate descriptive statistics about the stocks’ historical rates of return. Finally, you will create a variance-covariance matrix of the stocks’ returns.

Preliminaries

In your work on this assignment, make sure to abide by the collaboration policies of the course.

If you have questions while working on this assignment, please post them on Piazza! This is the best way to get a quick response from your classmates and the course staff.

Warm-up Problems

Work on these practice problems before class. We will discuss solutions in class and answer your questions.

1. Write a function print_squares(numbers) that prints the square of each value in the list numbers.

   Example:

   >>> print_squares([6,7,8])
   36
   49
   64
   

   Note: no return statement is required

2. Write a function print_acronym(words) that prints the first letter of each word in a list of words.

   Examples:

   >>> print_acronym(['boston', 'university'])
   bu
   >>> print_acronym(['strawberry', 'fields', 'forever'])
   sff
   >>> print_acronym(['thank', 'goodness', "it's", 'friday'])
   tgif
   >>>
   

   Note: to stay on the same line when printing, specify the end argument, i.e.: print(‘foo’,end=’‘)

3. At the console, create the following lists of numbers using the range function:

   >>> list(range(    ,    ))
   [2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
   
   >>> list(range(    ,     ,  ))
   [0, 7, 14, 21, 28, 35, 42, 49]
   
   >>> list(range(    ,     ,    ))
   [100, 97, 94, 91, 88, 85, 82, 79, 76, 73, 70, 
   67, 64, 61, 58, 55, 52, 49, 46, 43, 40, 37, 34, 
   31, 28, 25, 22, 19, 16, 13, 10, 7, 4, 1]
   

4. Write a function find_min(numbers) that processes a list of numbers, and returns the minimum value from that list.

   Examples:

   >>> find_min([6])
   6
   >>> find_min([6,8,5,7,4,9])
   4
   

   You may assume there is at least one value in the list.

   Hint: use an accumulator variable to hold on to the “minimum so far” as you go through the list of numbers.

5. Write a function fib(n) that returns a list of the first n Fibonacci numbers. In general, the Fibonacci number F(i) = F(i-1) + F(i-2)

   Examples:

   >>> fib(10)
   [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
   >>> fib(20)
   [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 
   233, 377, 610, 987, 1597, 2584, 4181]
   >>> fib(0)
   []
   >>> fib(1)
   [0]
   >>> fib(2)
   [0, 1]
   

   Note: use a definite loop, no recursion! Hint: start with special cases for n == 0 or n == 1

Task 1: Descriptive Statistics

50 points; individual-only

Do this task in a file called a3task1.py.

1. Write the function mean(values), that takes as a parameter a list of numbers, and calculates and returns the mean of those values. The mean is defined as:

   

   For example:

   >>> x = [4,4,3,6,7]
   >>> mean(x)
   4.8
   

2. Write the function variance(values), that takes as a parameter a list of numbers, and calculates and returns the population variance of the values in that list. The population variance is defined as: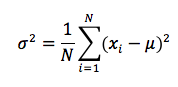

   

   For example:

   >>> x = [4,4,3,6,7]
   >>> variance(x)
   2.16
   

   Notes:

   • Your function must use a definite loop and the accumulator pattern to calculate the sum of squared deviations from the mean.
   • Re-use your code! You should call your existing mean function from within your variance function, and store the result in a local variable.

3. Write the function stdev(values), that takes as a parameter a list of numbers, and calculates and returns the population standard deviation of the values in that list. The population standard deviation is the square-root of the population variance.

   For example:

   >>> x = [4,4,3,6,7]
   >>> stdev(x)
   1.469693845669907
   

   Notes:

   • Re-use your code! You should call your existing variance function from within stdev. This function does not require the accumulator pattern.

4. Write the function covariance(x,y) that takes as parameters two lists of values, and calculates and returns the population covariance for those two lists. The population covariance is defined as: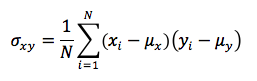

   

   For example:

   >>> x = [4,4,3,6,7]
   >>> y = [6,7,5,10,12]
   >>> covariance(x,y)
   3.8
   

5. Write the function correlation(x,y) that takes as parameters two lists of values, and calculates and returns the correlation coefficient between these data series. The correlation coefficient is defined as: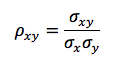

   

   For example:

   >>> x = [4,4,3,6,7]
   >>> y = [6,7,5,10,12]
   >>> correlation(x,y)
   0.9915217942181532
   >>> correlation(list(range(10)), list(range(10,0,-1)))
   -0.9999999999999998
   

6. Write the function rsq(x,y) that takes as parameters two lists of values, and calculates and returns the square of the correlation between those two data series, which is a measure of the goodness of fit measure to explain variation in y as a function of variation of x.

   >>> x = [4,4,3,6,7]
   >>> y = [6,7,5,10,12]
   >>> rsq(x,y)
   0.9831154684095857
   

   Additional Example: we expect no correlation and very low r-square between randomly selected data values. This test uses two lists of random numbers. Notice the very low r-squared.

   >>> import random
   >>> a = list(range(30))
   >>> b = list(range(30))
   >>> random.shuffle(a)
   >>> random.shuffle(b)
   >>> a
   [6, 24, 29, 8, 20, 7, 28, 23, 14, 11, 25, 19, 12, 17, 2, 0, 26, 9, 10, 16, 4, 13, 22, 5, 15, 18, 21, 1, 27, 3]
   >>> b
   [17, 22, 25, 29, 27, 7, 11, 19, 26, 16, 0, 9, 21, 18, 3, 24, 8, 10, 20, 4, 13, 6, 28, 14, 2, 5, 23, 12, 15, 1]
   >>> correlation(a,b)
   0.12880978865406006
   >>> rsq(a,b)
   0.016591961653103622
   

7. Write the function simple_regression(x,y) that takes as parameters two lists of values, and calculates and returns the regression coefficients between these data series. The function should return a list containing two values: the intercept and regression coefficients, α and β.

   The regression coefficient and intercept are defined as:

   

   For example:

   >>> x = [4,4,3,6,7]
   >>> y = [6,7,5,10,12]
   >>> simple_regression(x,y)
   (-0.44444444444444287, 1.759259259259259)
   

Task 2: Stock Returns and Statistics

50 points; individual-only

Preliminaries

Do this task in a file called a3task2.py.

1. Write a function calc_returns(prices). This function will process a list of stock prices and calculate the periodic returns. The function should assume that the oldest price is in prices[0] and latest price in prices[-1]. The function should use a loop and accumulator pattern to accumulate a list of returns for periods 1 to n – there is no return for period 0.

   The periodic rate of return is calculated as the rate of change in price from the previous period, i.e.,

   

   For example:

   >>> prices = [100,110,105,112,115]
   >>> returns = calc_returns(prices)
   >>> print(returns)
   [0.10000000000000009, -0.045454545454545414, 0.06666666666666665, 0.02678571428571419]
   

   Notes:

   • For N stock prices, you will generate a list of N-1 periodic returns.

   • The function calc_prices should not print any output, but rather creates and returns a list of periodic rates of return.

   • When computing with binary floating point numbers, there is a small representational error which might result in an unexpected value in the insignificant digits (e.g., (110 - 100) / 100 gave a result of 0.10000000000000009.) Do not be alarmed by this small error!

   • The values in the list of returns will be unformatted floating-point numbers; we’ll do the formatting part later in a separate function.

2. Write a function process_stock_prices_csv(filename). This function will process a data file containing stock price data, and return a list of stock prices.

   The format of the file is that each line is a discrete record. The lines in this file are in CSV (“Comma Separated Values”) format. Here is an sample CSV file containing stock prices:

       Date,Open,High,Low,Close,Adj Close,Volume
       2012-01-10,60.844284,60.857143,60.214287,60.462856,54.395779,64549100
       2012-01-11,60.382858,60.407143,59.901428,60.364285,54.307095,53771200
       2012-01-12,60.325714,60.414288,59.821430,60.198570,54.158012,53146800
       2012-01-13,59.957142,60.064285,59.808571,59.972858,53.954945,56505400
       2012-01-17,60.599998,60.855713,60.422855,60.671429,54.583416,60724300
   

   The first row contains header information, which we will discard. Each line after the first line is a record for one date. For this assignment, we only care about the next-to-last value (“Adj Close”), which is the adjusted close price on that date.

   Your function should return the stock prices as a list. Here is an algorithm to process this CSV file:

   • Create an empty list to hold the prices (i.e., set a list as an accumulator variable).
   • Open the file for reading using the built-in function open(filename).
   • Read and discard the first line (i.e., the headers).
   • Use a for loop to process the rest of the file. For every remaining line in the file, parse that line to obtain the last element, which is the price. Convert this price into a floating-point number (float), and append it to the list.

   Here is an example of client code to run this file. Note that the filename will depend on where you save the file on your computer. This filename works for my computer only!

   >>> filename = './AAPL.csv'
   >>> prices = process_stock_prices_csv(filename)
   >>> # prices is now a list containing the only adjusted closing prices for each day.
   

3. Write a function stock_report(filenames) as a client program to process stock prices and display descriptive statistics about the stocks. This program will process the list of filenames, each of which is a .CSV file containing stock price data in the Yahoo Finance format (for the same time periods), as well as the the stock market index (^SPC). The finished version of the function must return a string containing the entire report, i.e., several outputs, neatly formatted, etc.

   Your client program should do the following tasks for each stock:

   • Use your function process_stock_prices_csv to read the stock price data from the file, and obtain a list containing only the stock prices (no other fields).

   • Calculate the stock returns by calling your calc_returns(prices) on the list of the stock’s prices to obtain a list of returns.

   • Find the mean and standard deviation of returns, and print them out in a nicely formatted table. You should re-use your functions from Task 1. It would be helpful to import your functions from Task 1, using this line:

     from a3task1 import *
     

     which will give you access to all of your statistical functions from Task 1.

   We want to compare each stock to the stock market index (use SPY for the SPY 500 index), to see how this stock might affect a portfolio’s expected return. (If you are not familiar with it, here is a brief reading about the Capital Asset Pricing Model).

   You will use your functions from Task 1 to find the covariance with the market return (SPY or ^SPC or VTSMX), the correlation coefficient, the r-square statistic, and the regression coefficients (beta describes this stocks’ market risk, i.e., how much this stock’s return varies in relation to the market as a whole).

   Finally, your function should create a report that is well-formatted. You may decide what kind of formatting looks good to you, but here is a sample:

       >>> filenames = ['AAPL.csv', 'GOOG.csv', 'IBM.csv', 'SPY.csv']
       >>> stock_report(filenames) # note, this function will return a string
       '''
       Calculated returns for 4 stocks.
   
       Descriptive statistics for daily stock returns:
       Symbol:       AAPL       GOOG        IBM        SPY 
       Mean:       0.00107    0.00062    0.00035    0.00041 
       StDev:      0.01972    0.01848    0.01391    0.01281 
       Covar:      0.00015    0.00015    0.00012    0.00016 
       Correl:     0.60966    0.64289    0.69672    1.00000 
       R-SQ:       0.37169    0.41331    0.48542    1.00000 
       Beta:       0.39625    0.44585    0.64166    1.00000 
       Alpha:     -0.00001    0.00013    0.00018    0.00000 
       '''
   

   Hints/Notes:

   • This sample uses daily return data. Your results will differ from the sample output! This is expected. The daily mean return will be approximately 1/250 of the annual return, and the daily standard deviation will be approximately 1/sqrt(250) of the annual standard deviation.

   • This code assumes that the “market reference” (SPY) is the last .csv file in the list. You should do the same.

   • Before trying to build this table, call each of the statistical functions and save the result in a variable. While you are testing, you should print out the variables to ensure you know each function works.

   • Build the table one line at a time, using string concatenation (i.e., +=). When the function is done, return the string. The finished function shuold not print!

   • This sample uses number formatting to limit the number of digits after the decimal point. Read about it in the .PPT slides from class.

Submitting Your Work

Log in to GradeScope to submit your work.

Be sure to name your files correctly!

Under the heading for Assignment 3, attach each of the required files to your submission.

When you upload the files, the autograder will test your functions/programs.

Notes:

• You must upload your .csv (stock price data files) as well as your .py files.
• You may resubmit multiple times, but only the last submission will be graded.