Title
Overview
- Implicit representations
- Discrete implicit representations
- Explicit representations: parametric curves
- Discrete curves
Implicit Representations
Some basic examples
- How can we define a unit circle centered at the origin?
- In words: All points that are at distance one from the origin
- Mathematically: \(\{ \vec{x} = (x,y) \in \R^2 \mid \sqrt{x^2 + y^2} = 1 \}\)
- Implicit Representation
- Kernel of function \(F: \R^n \to \R\), i.e. \(\{\vec{x} \in \R^n \mid F(\vec{x}) = 0\}\)
- Unit circle: \(F(x,y) = \sqrt{x^2 + y^2} - 1\)
- Circle of radius \(r\) centered at \((c_x, c_y)\): \[F(x,y) = \sqrt{(x-c_x)^2 + (y-c_y)^2} - r\]
- Unit sphere: \(F(x,y,z) = \sqrt{x^2 + y^2 + z^2} - 1\)
Zero set defines curve/surface
- Kernel of function \(F: \R^n \to \R\)
- Notion of distance not crucial, only zero set is relevant
- Different functions \(F\) can yield the same geometry
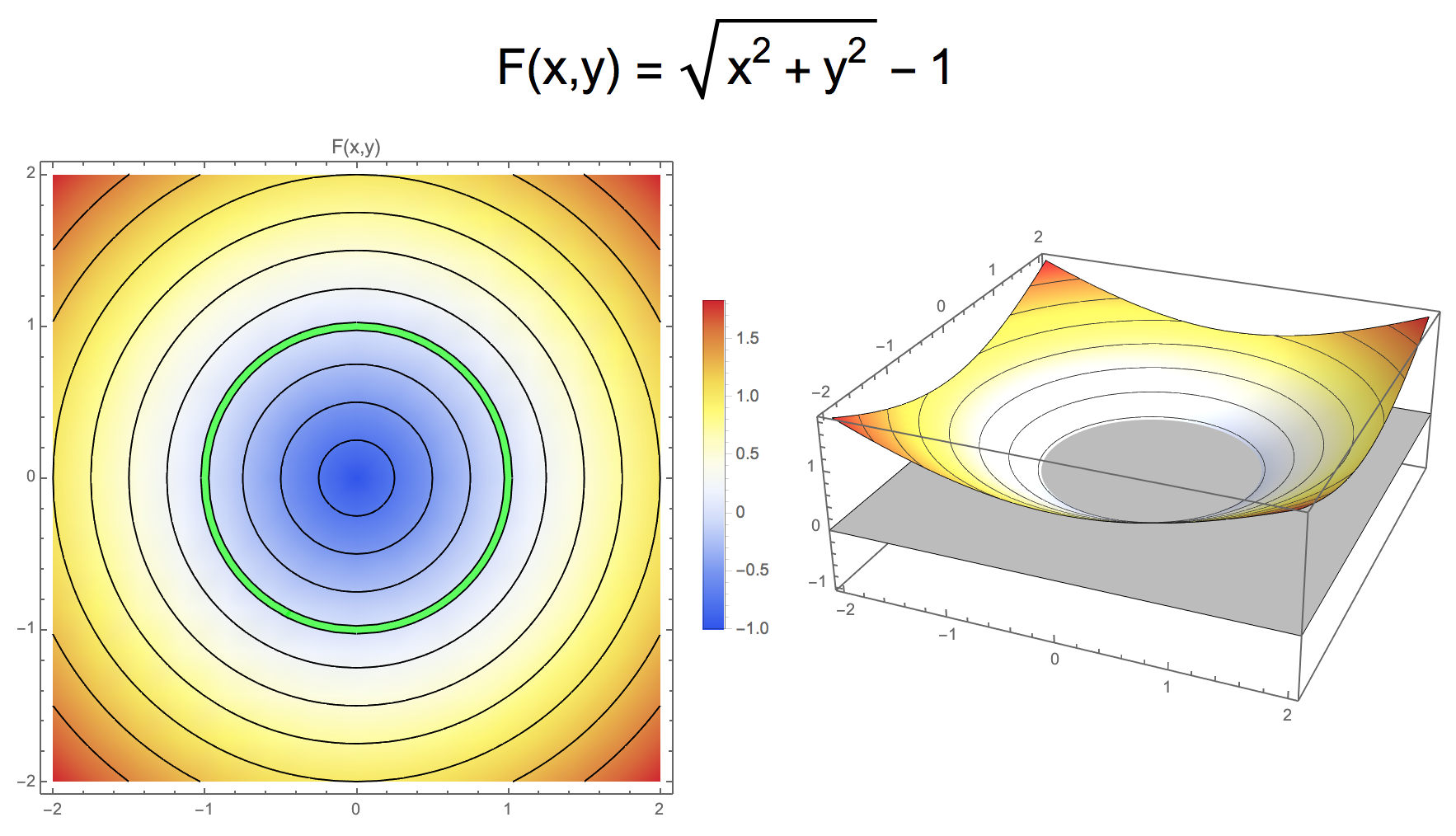
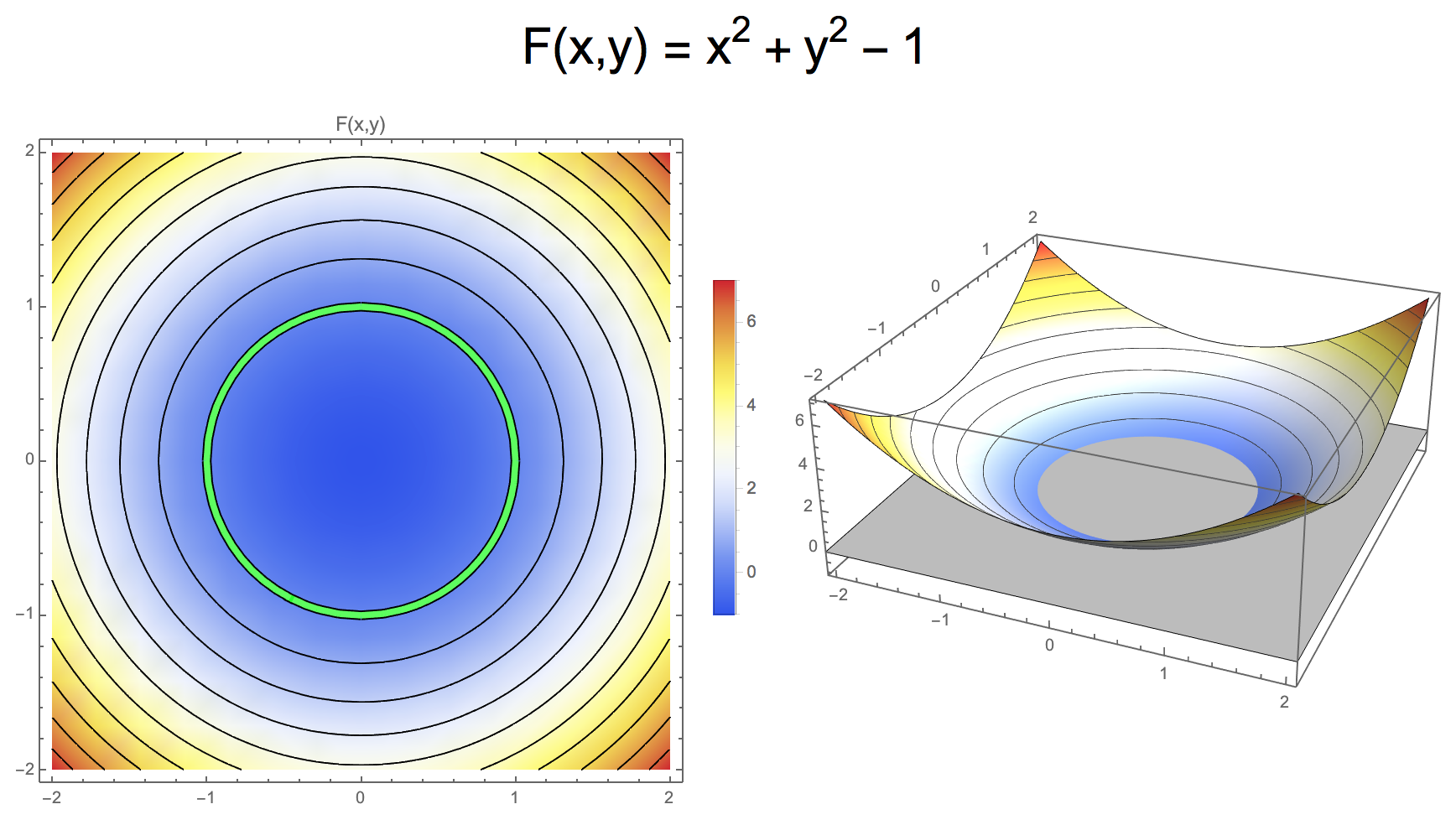
- Example: \(F(x,y) = \sqrt{x^2 + y^2} - 1\) or \(F(x,y) = x^2 + y^2 - 1\)
Implicit curve as a level set
- Level set of 2D function defines 1D curve
- different level values define different curves
Wikipedia: Implicit Curve
Implicit surface as a level set
- Level set of a 3D function defines a 2D surface
Wikipedia: Implicit Surface
Gradient of Implicit Function
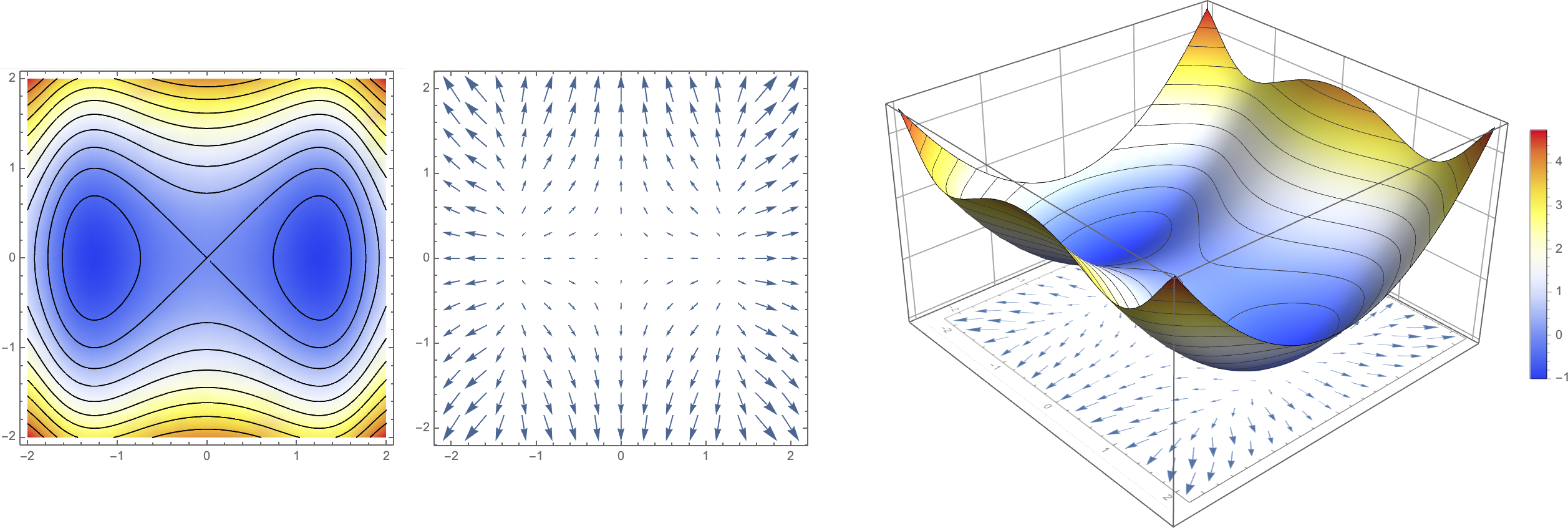
- Gradient of function \(F: \R^n \to \R\) is defined as \[\nabla F = \left[ \frac{\partial F}{\partial x_1},\, \frac{\partial F}{\partial x_2},\, \cdots,\, \frac{\partial F}{\partial x_n} \right]^T\]
Wikipedia: Gradient
Gradient of Implicit Function
- Gradient of function \(F: \R^n \to \R\) is defined as \[\nabla F = \left[ \frac{\partial F}{\partial x_1},\, \frac{\partial F}{\partial x_2},\, \cdots,\, \frac{\partial F}{\partial x_n} \right]^T\]
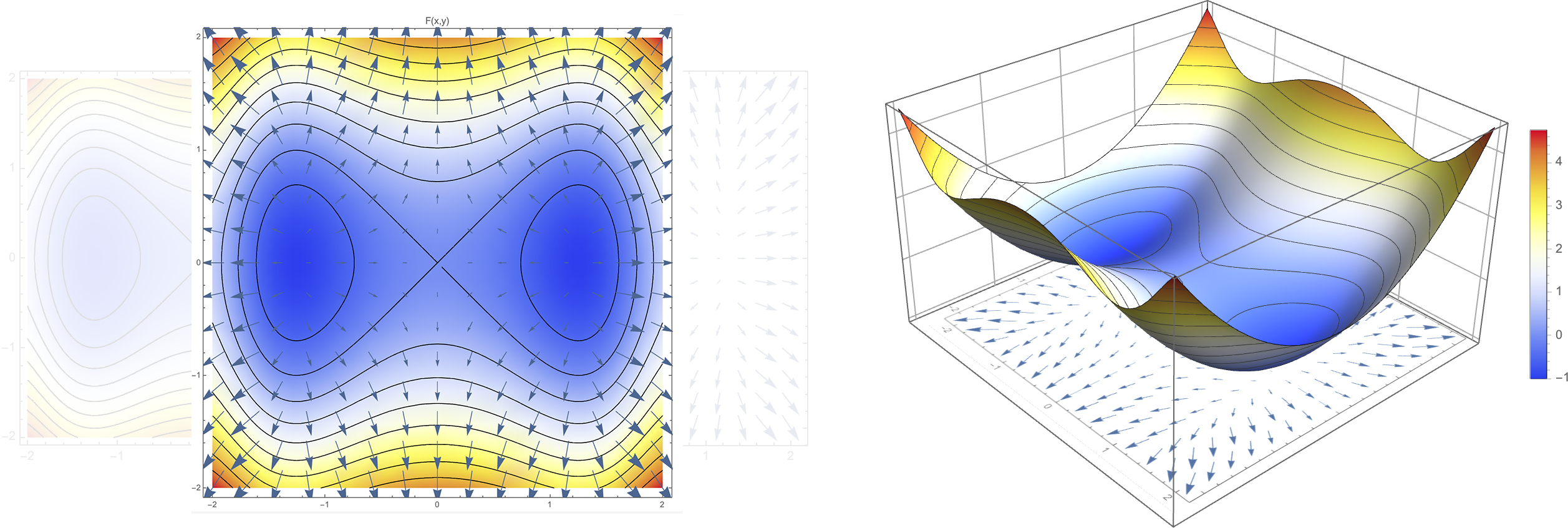
Gradient \(\nabla F\) is orthogonal to iso-surface
Wikipedia: Gradient
Signed Distance Function (SDF)
- Special case of an implicit representation
- \(F(\vec{x})\) gives signed distance to closest point on level surface
- Convention for sign: \(F(\vec{x}) < 0\) for interior, \(F(\vec{x}) > 0\) for exterior
- \(\nabla F\) is unit surface normal
- level sets are at constant offset distance
- SDF of circle: \[F(x,y) = \sqrt{x^2 + y^2} - 1\]
- SDF of sphere \[F(x,y,z) = \sqrt{x^2 + y^2 + z^2} - 1\]
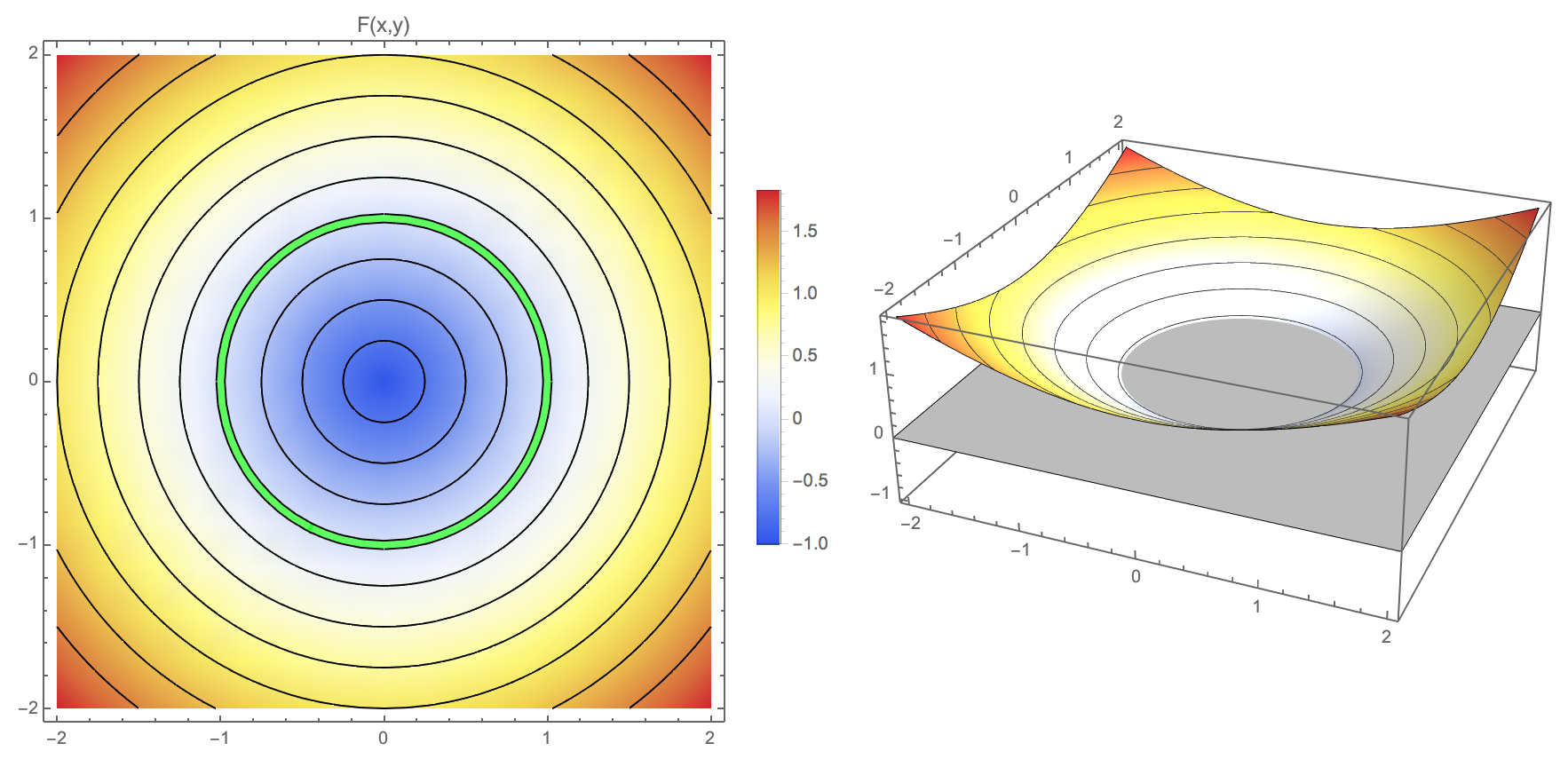
Modeling with Implicit Representations?
- Guess the shape of the curve! \[ F(x,y) = \left(y-\sqrt[3]{x^2}\right)^2 + x^2 - 1\]
Modeling with Implicit Representations?
- Guess the shape of the curve! \[ F(x,y) = \left(y-\sqrt[3]{x^2}\right)^2 + x^2 - 1\]
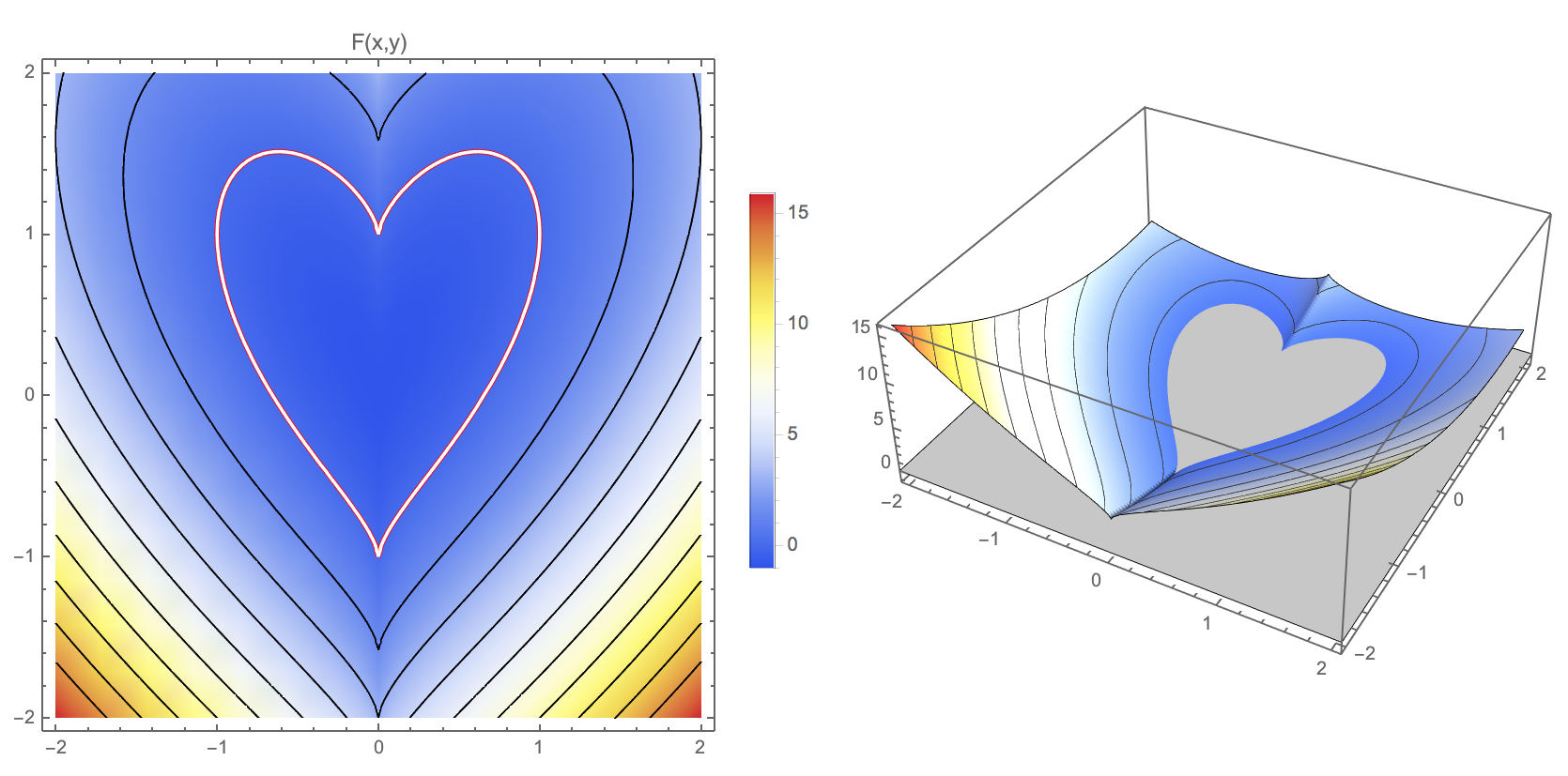
Discrete Implicit Representation
- An implicit function \(F\) can be discretized by sampling
- Reconstruct continuous function from discrete values
- Example:
Discrete Implicit Representation
- An implicit function \(F\) can be discretized by sampling
- Reconstruct continuous function from discrete values
- Example: Piecewise linear representation on regular grid
2D Marching Squares Algorithm
Classify grid nodes as inside/outside
- Is \(F(x_{i,j})\) below or above iso-value?
Classify cell: \(2^4 = 16\) configurations
- in/out for each corner
Determine vertex positions
- linear interpolation of grid values along edges
Determine contour edges
- look-up table for edge configuration
2D Marching Squares Algorithm
Application example
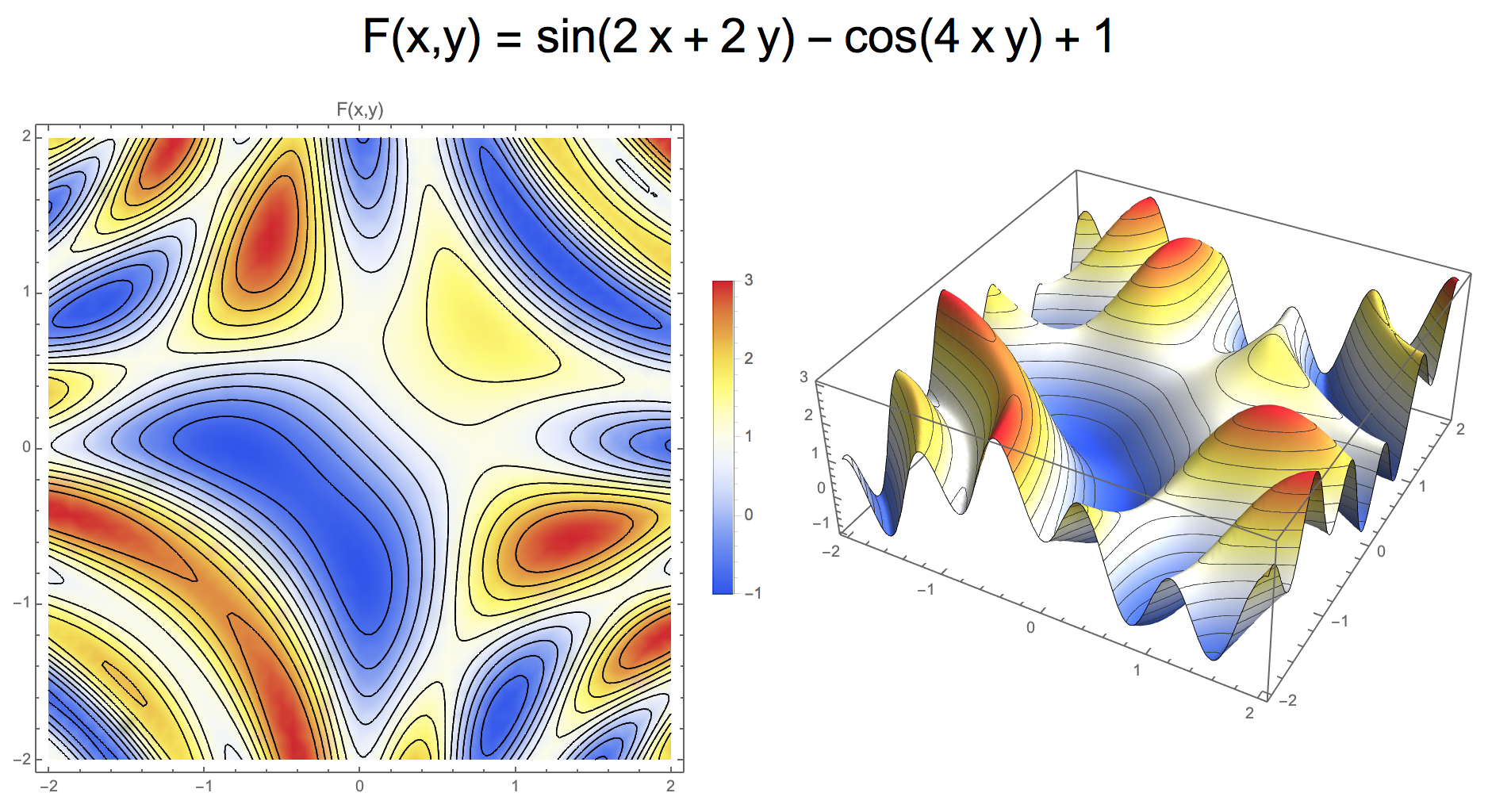
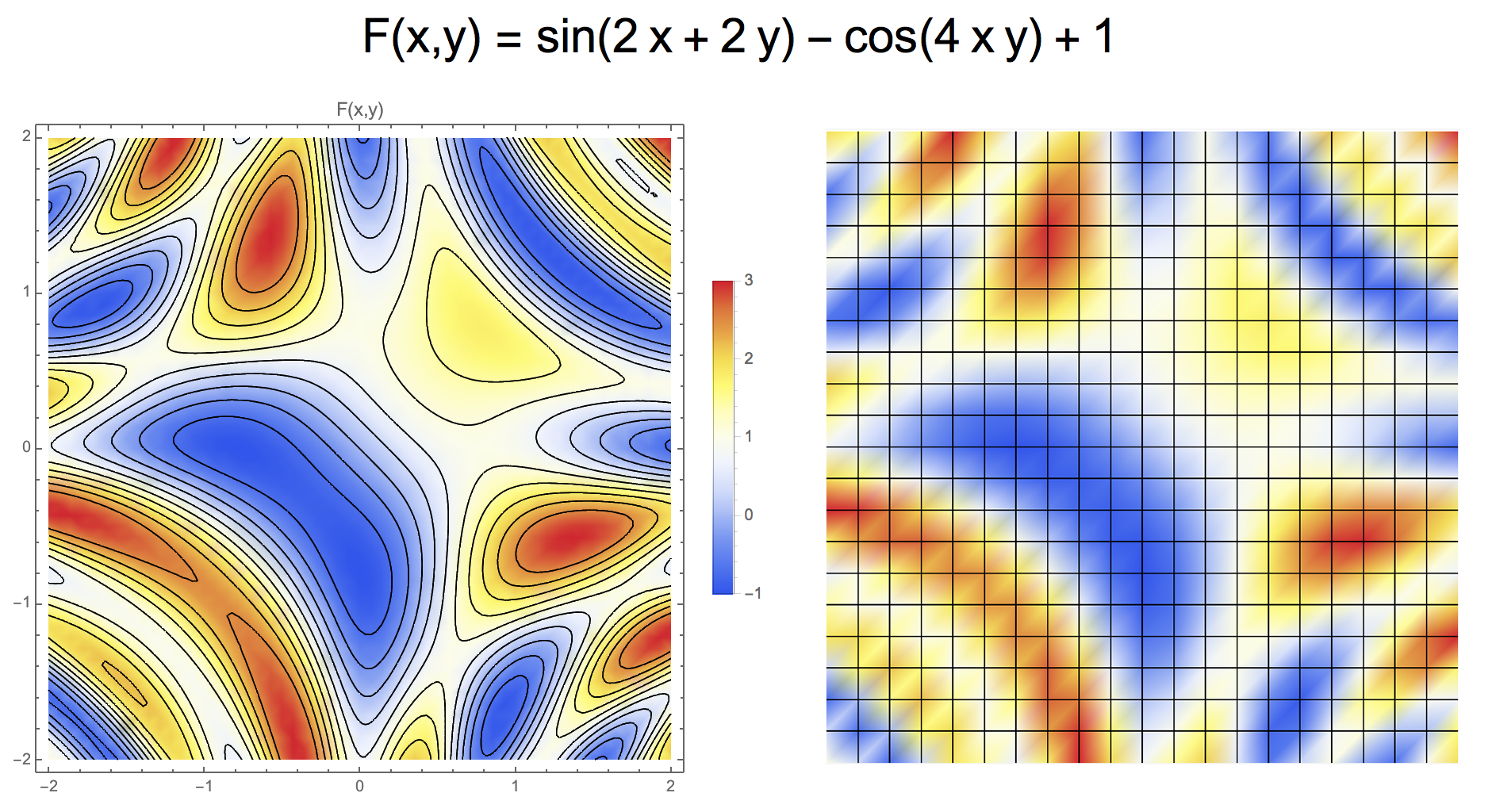
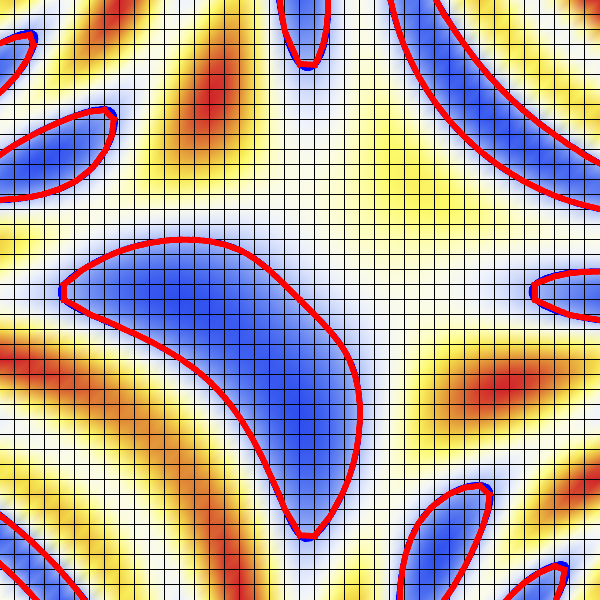
- Example: \(F(x,y)= \sin(2x + 2y) - \cos(4xy) + 1 = 0\)
- Increasing resolution reduces reconstruction error

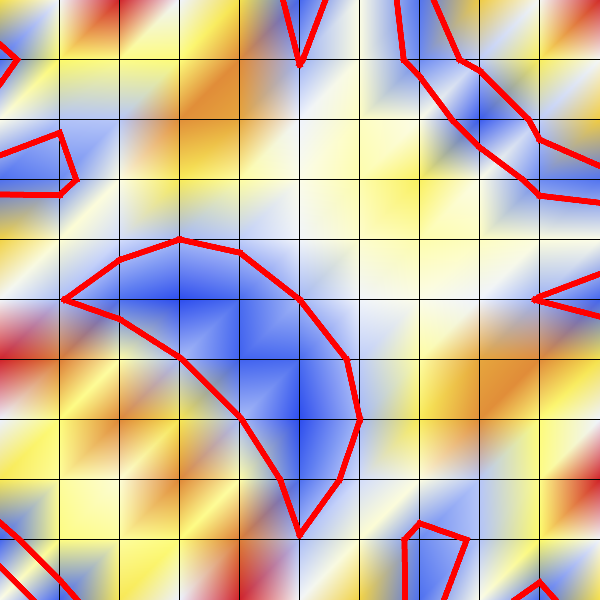
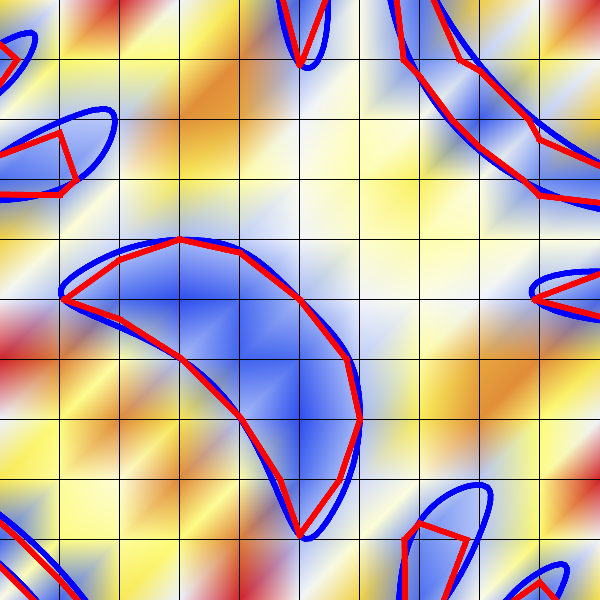
Application example
- Example: \(F(x,y)= \sin(2x + 2y) - \cos(4xy) + 1 = 0\)
- Increasing resolution reduces reconstruction error

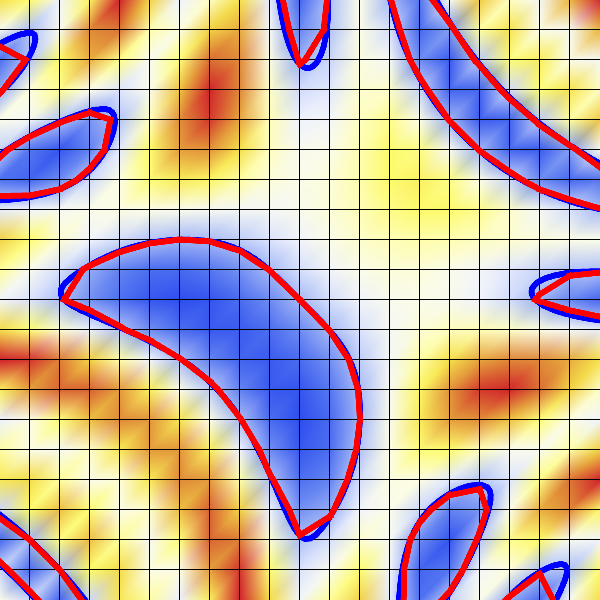
3D Marching Cubes Algorithm
- Classify grid nodes as inside/outside
- Is \(F(x_{i,j,k})\) below or above iso-value?
- Classify cell: \(2^8 = 256\) configurations
- in/out for each corner
- Determine vertex positions
- linear interpolation of grid values along edges
- Determine contour triangles
- look-up table for triangle configuration
3D Marching Cubes Algorithm
- Determine vertex positions
- linear interpolation of grid values along edges
3D Marching Cubes Algorithm
- Determine contour triangles
- look-up table for triangle configuration
3D Marching Cubes Algorithm
Implicit Representations
- Pros:
- Easy to determine if a point is inside or outside (e.g. for collision detection)
- Handles topology changes with ease
- Cons:
- Hard to sample the curve/surface (e.g. for rendering)
- Hard to deform the surface (e.g. for deformation)
Explicit Representations: Parametric Curves
Parametric Curve Representation
Parametric representation \(\vec{x} \colon [a,b] \subset \R \to \R^2\) (or \(\R^3\)) \[\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\]
Curve is defined as image of interval \([a,b]\) under parameterization function \(\vec{x}\).
Unit circle: \(\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}} = \matrix{\cos\of{t} \\ \sin\of{t}}, t \in [0,2\pi]\)
Parametric Representation
- Parametric representation \(\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\)
Parametric Representation
- Guess the shape of the curve! \[\vec{x}\of{t} = \matrix{\sin^3(t) \\ \frac{1}{16}(13\cos(t) - 5 \cos(2t) - 2 \cos(3t)-\cos(4t))}\]
Parametric Representation
Tangent & Normal
Parametric representation of planar curve \(\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\)
First derivative defines the tangent vector \[\vec{t} = \vec{x}’\of{t} := \frac{\mathrm{d} \vec{x}\of{t}}{\mathrm{d} t} = \matrix{ \mathrm{d}x\of{t} / \mathrm{d} t \\ \mathrm{d}y\of{t} / \mathrm{d} t}\]
The curve normal vector is \[\vec{n} = \text{Rot}(90) \frac{\vec{t}}{\| \vec{t} \|}\]
Tangent & Normal
Example: \(\vec{x}\of{t} = (1+\cos(t)) \matrix{\cos(t) \\ \sin(t)}\)
Curve as Particle Trajectory
Curve parameter \(t\) is time
\(\vec{x}\of{t}\) defines the position of particle at time \(t\)
Tangent \(\vec{x}’\of{t}\) defines the velocity vector at time \(t\)
Length (magnitude) of tangent vector is particle speed
Parametric Curve Properties
- A parametric curve \(\vec{x}\of{t}\) is
- simple: \(\vec{x}\of{t}\) is injective (no self-intersections)
- differentiable: \(\vec{x}’\of{t}\) is defined for all \(t \in [a,b]\)
- regular: \(\vec{x}’\of{t} \neq \vec{0}\) for all \(t \in [a,b]\)
- Which of the following are simple, differentiable, regular?
Re-parameterization
- We can represent the same geometry with different parameter functions
- For example, the same curve is defined for \(t \in [0,1]\) by the functions \[\vec{x}_1\of{t} = \matrix{\sin(4 \pi t) \\ \cos(2 \pi t)} \;\text{ and }\; \vec{x}_2\of{t} = \matrix{\sin(4 \pi t^2) \\ \cos(2 \pi t^2)}\]
- In other words, the image of \([0,1]\) under \(\vec{x}_1\) and \(\vec{x}_2\) is equivalent
- However: \(\vec{x}_1\of{t} \neq \vec{x}_2\of{t}\)!
Re-parameterization
- We can map from \(\vec{x}_1\) to \(\vec{x}_2\) using a re-parameterization function \(u\)
- In our example, we have \(u \colon [0,1] \to [0,1]\) with \(u(t) = t^2\)
- If \(\vec{x}_1(t) = \vec{c}(t)\), then \(\vec{x}_2(t) = \vec{c}(u(t))\)
Re-parameterization
- We can map from \(\vec{x}_1\) to \(\vec{x}_2\) using a re-parameterization function \(u\)
- In our example, we have \(u \colon [0,1] \to [0,1]\) with \(u(t) = t^2\)
- If \(\vec{x}_1(t) = \vec{c}(t)\), then \(\vec{x}_2(t) = \vec{c}(u(t))\)
- Parameter intervals do not need to be identical!
- For example, if \(\vec{x}_1 \colon [a,b] \to \R^2\) and \(\vec{x}_2 \colon [c,d] \to \R^2\) define the same curve, we can define a re-parameterization function \(u \colon [a,b] \to [c,d]\) such that \(\vec{x}_1(t) = \vec{x}_2(u(t))\)
Quiz
- Which of the following parametric curves have the same geometry as \(\trans{[ \cos(t), \sin(t)]}, t \in [0, \pi]\)?
- \(\matrix{\cos(2t) \\ \sin(2t)} ,\; t \in [ 0, 2\pi]\)
- \(\matrix{t \\ \sqrt{1-t^2} } ,\; t \in [-1, 1 ]\)
- \(\matrix{\cos(t^2) \\ \sin(t^2)} ,\; t \in [0, \pi ]\)
- \(\matrix{\sin(t) \\ -\cos(-t)} ,\; t \in [\frac{\pi}{2}, \frac{3\pi}{2}]\)
Discrete Explicit Representation
- Sample the parameter interval \([a,b]\), e.g., at parameters \(t_i = a + i \frac{b-a}{n},\; i = 0, \ldots, n\)
- Then the polyline through the points \(\vec{x}\of{t_i}\) is a piecewise linear approximation of the curve \(\vec{x}\)
- With increasing \(n\), the polyline converges to the curve
Length of a Curve
- How can we measure the length of a continuous curve?
- We know how to measure the length of a polyline!
- Let \(t_i = a + i \Delta t\) and \(\vec{x}_i = \vec{x}\of{t_i}\)
- Polyline chord length \[ L = \sum_i \norm{ \Delta \vec{x}_i } \;,\qquad \Delta\vec{x}_i := \vec{x}_{i+1} - \vec{x}_i \]
- Curve arc length \[ \sum_i \norm{ \Delta \vec{x}_i } = \sum_i \norm{ \frac{\Delta \vec{x}_i}{\Delta t} } \Delta t \quad\stackrel{\Delta t \to 0}{\longrightarrow}\quad \int_a^b \norm{\vec{x}’(t)} \mathrm{d}t \]
Example: Length of Circle
\[\vec{x}\of{t} = \matrix{\cos\of{t} \\ \sin\of{t}} \qquad \vec{x}’\of{t} = \matrix{-\sin\of{t} \\ \cos\of{t}}\]
Arc Length Parameterization
- We see that a curve can be parameterized in different ways. But is there a unique, canonical way to parameterize a curve?
- Yes! It’s called arc length parameterization
- Parameterize curve \(\vec{x}(s)\) over interval \([0, L]\) such that length from \(\vec{x}(0)\) to \(\vec{x}(s)\) is equal to \(s\) \[\int_0^s \norm{\vec{x}'(t)}\func{d}t \;=\; s\]
Arc Length Parameterization
- Intuitively, think about a rope of length \(L = \int \norm{\vec{x}’} \mathrm{d}t\) that is bent (but not stretched or compressed!) to assume the shape of the curve
- Curves parameterized with respect to arc length have some useful properties
- Unit speed: \(\norm{ \vec{x}'(s) } = 1\)
- Orthogonality: \(\vec{x}'(s) \cdot \vec{x}''(s) = 0\)
Curvature
- Curvature is a measure of how much the curve deviates from a straight line
- This can be quantified by looking at how much the tangent/normal varies as we traverse the curve
- If a curve is parameterized by arc length, then curvature \(\kappa\) is defined through the second derivative w.r.t. arc length \(s\): \[ \vec{t}'(s) = \vec{x}''(s) = \kappa\of{s} \vec{n}(s) \]
Curvature
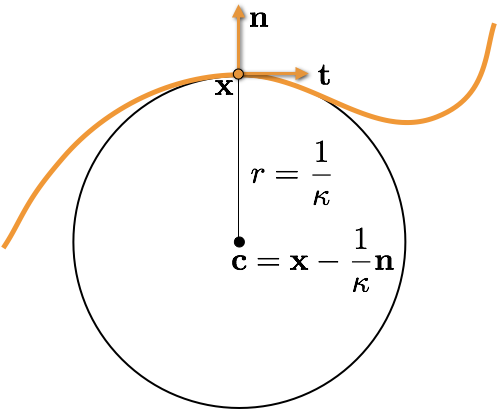
- The osculating circle at point \(\vec{x}\) is the circle tangent to the curve at \(\vec{x}\) that best approximates the curve locally
(German: Schmiegkreis) - Its center is given as \(\vec{x} - \frac{1}{\kappa} \vec{n}\), where \(\kappa\) is the signed curvature and \(\vec{n}\) is the normal at \(\vec{x}\).
- Its radius is the inverse of the absolute curvature: \(r=1/|\kappa|\)