Lecture 3D Geometry Processing

Discrete Differential Geometry

Prof. Edward Chien

Geometry Processing & Computer Graphics

Triangle Meshes

Connectivity / Topology
- Vertices \(\mathcal{V} = \{ v_1, \dots, v_n \}\)
- Edges \(\mathcal{E} = \{ e_1, \dots, e_k \}\), \(e_i \in \mathcal{V} \times \mathcal{V}\)
- Faces \(\mathcal{F} = \{ f_1, \dots, f_m \}\), \(f_i \in \mathcal{V} \times \mathcal{V} \times \mathcal{V}\)

Geometry
- Vertex positions \(\{ \vec{p}_1, \dots, \vec{p}_n \}\), \(\vec{p}_i \in \R^3\)

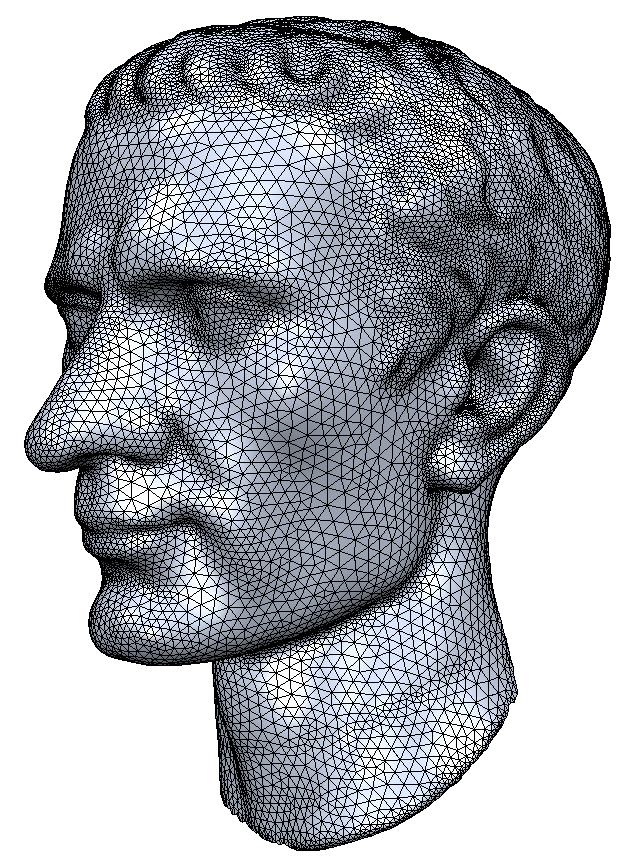
Why Triangle Meshes?

Triangle meshes can represent arbitrary surfaces

Why Triangle Meshes?

Triangle meshes can represent arbitrary surfaces
Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)

Why Triangle Meshes?

Triangle meshes can represent arbitrary surfaces
Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
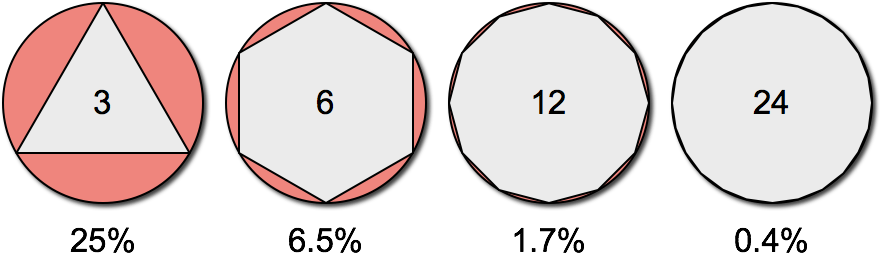
Approximation error inversely proportional to #triangles

Why Triangle Meshes?

Triangle meshes can represent arbitrary surfaces
Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
Approximation error inversely proportional to #triangles
Adaptive tesselation can adapt to surface curvature

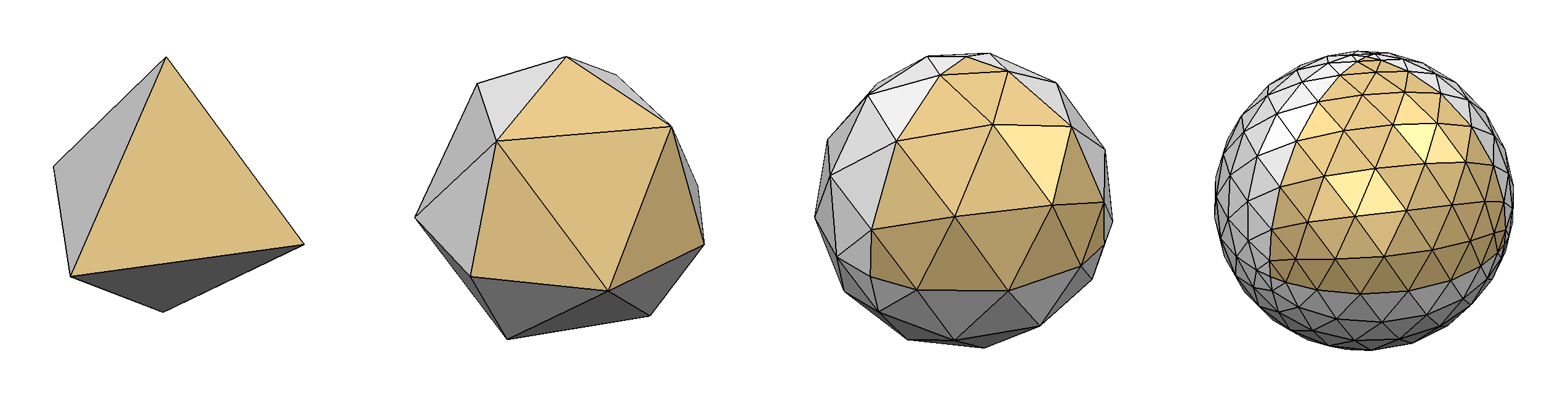
Why Triangle Meshes?

Triangle meshes can represent arbitrary surfaces
Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
Approximation error inversely proportional to #triangles
Adaptive tesselation can adapt to surface curvature
Simple primitives can be processed efficiently by CPU/GPU

Mathematical Manifold Definition

A topological space \(M\) is a topological \(n\)-manifold if:

For manifold with boundaries replace \(\mathbb{R}^n\) with \(\mathbb{H}^n\).

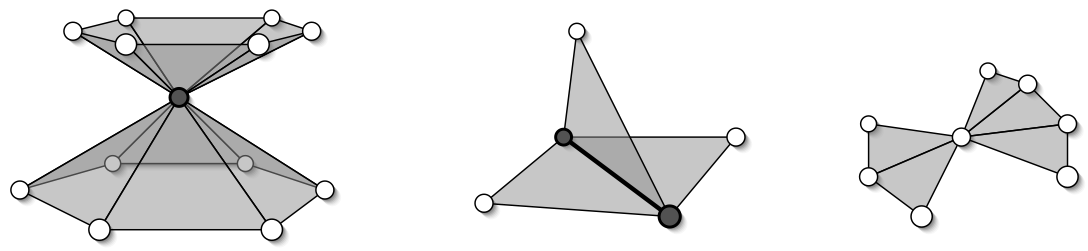
Two-Manifold Surfaces

Local neighborhoods are disk-shaped
Guarantees meaningful neighborhood enumeration
Required by most algorithms
Non-manifold examples:

Mesh Data Structures

2D Mesh Combinatorics: Euler’s Polyhedron Formula

\[V - E + F = \chi = 2-2g-n\]

\(g\) denotes the number of “handles”
\(n\) denotes the number of boundaries
\(\chi \approx 0\) relative to \(V,E,F\) for the vast majority of meshes

\[ 2E \approx 3F \approx 6V \] (first relation is equality if there are no boundaries)

Face Set

Face Set is a standard file format for triangle meshes (e.g. STL format)
Memory consumption
36 B/f = 72 B/v

Indexed Face Set

Indexed Face Sets are used for many file formats (e.g. OFF, OBJ, VRML)
Memory consumption
12 B/v + 12 B/f = 36 B/v

Face-Based Connectivity

Store connectivity per face
Memory consumption
16 B/v + 24 B/f = 64 B/v
Non-constant element size for general polygonal meshes
Edges not represented

Edge-Based Connectivity

Store connectivity per edge
Memory consumption
16 B/v + 4 B/f + 32 B/e = 120 B/v
Edges explicitly represented
Missing edge orientation leads to case distinctions during traversal

Halfedge-Based Connectivity

Store connectivity per halfedge
Memory consumption
16 B/v + 4 B/f + 20 B/h = 144 B/v
(can be reduced to 96 B/v)
Edges & halfedges explicitly represented
No case distinctions during traversal!

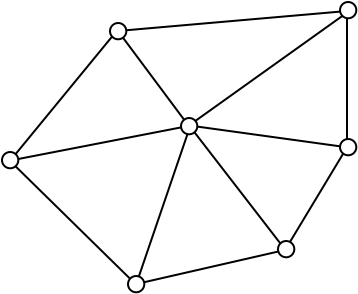
One-Ring Traversal

Simple one-ring traversal without case distinctions:
1. Start at vertex
2. Outgoing halfedge
3. Opposite halfedge
4. Next halfedge
5. Opposite halfedge
6. Next halfedge
7. …

Halfedge-Based Libraries

CGAL
- http://www.cgal.org
- Computational geometry
OpenMesh
- http://www.openmesh.org -Mesh processing
Surface_mesh
- http://graphics.uni-bielefeld.de/publications/imr11/
- Like OpenMesh, but without templates

Triangle Meshes

Connectivity / Topology
- Vertices \(\mathcal{V} = \{ v_1, \dots, v_n \}\)
- Edges \(\mathcal{E} = \{ e_1, \dots, e_k \}\), \(e_i \in \mathcal{V} \times \mathcal{V}\)
- Faces \(\mathcal{F} = \{ f_1, \dots, f_m \}\), \(f_i \in \mathcal{V} \times \mathcal{V} \times \mathcal{V}\)

Geometry
- Vertex positions \(\{ \vec{p}_1, \dots, \vec{p}_n \}\), \(\vec{p}_i \in \R^3\)

Normal Vectors

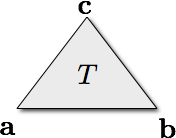
Triangle normal \[ \vec{n}(T) = \frac{\left(\vec{b}-\vec{a}\right) \times \left(\vec{c}-\vec{a}\right)} {\norm{\left(\vec{b}-\vec{a}\right) \times \left(\vec{c}-\vec{a}\right)}} \]

Vertex normal
- Average of incident triangles’ normals \(\vec{n}(T_i)\)
- Weighted by area or opening angle \(w(T_i)\)
\[ \vec{n}(V) = \frac{ \sum_{T_i \ni V} w(T_i) \, \vec{n}(T_i)} { \norm{ \sum_{T_i \ni V} w(T_i) \, \vec{n}(T_i)} } \]

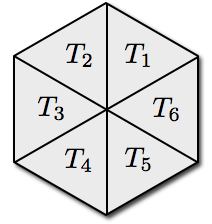
Vertex Normals

Discrete Curvatures

How to discretize curvatures on a mesh?
- Zero curvature within triangles
- Infinite curvature at edges / vertices
- Point-wise definition does not make sense

Approximate differential properties at point \(\vec{x}\) as average over local neighborhood \(A(\vec{x})\)
- \(\vec{x}\) is a mesh vertex
- \(A(\vec{x})\) is within one-ring neighborhood

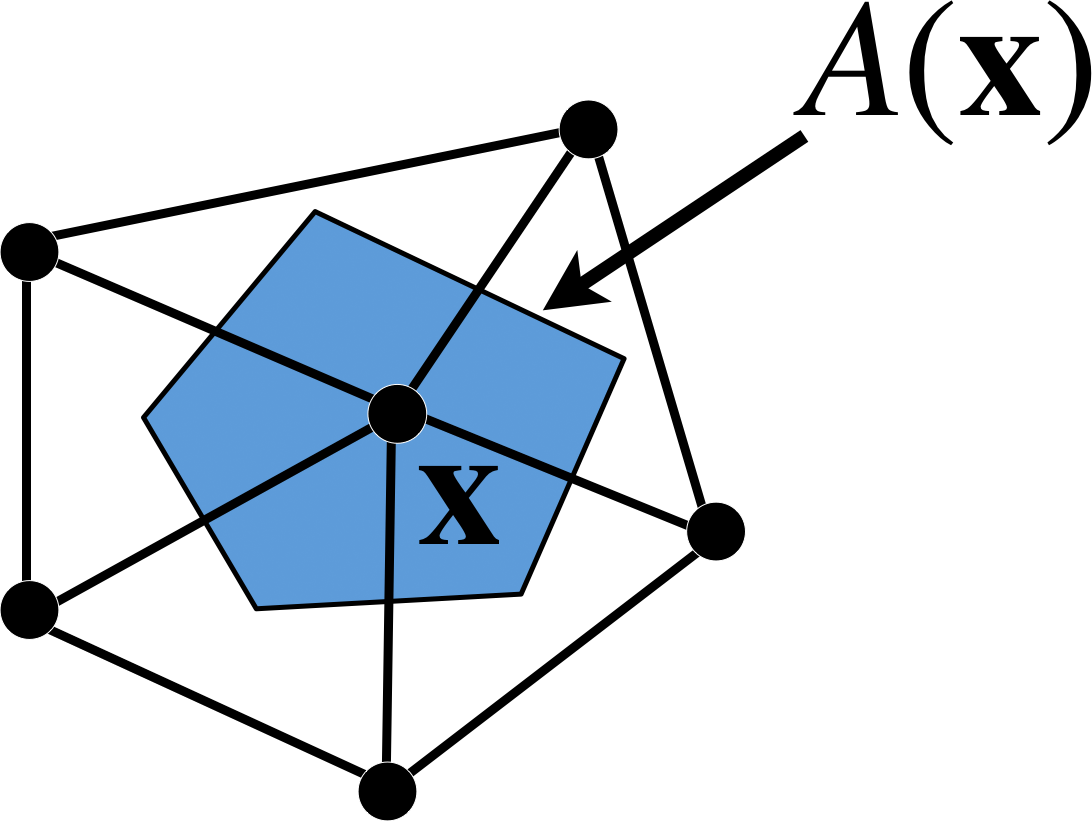
Discrete Curvatures

How to discretize curvatures on a mesh?
- Zero curvature within triangles
- Infinite curvature at edges / vertices
- Point-wise definition does not make sense

Approximate differential properties at vertex \(v\) as average over local neighborhood \(A(v)\) \[C\of{v} \;\approx\; \frac{1}{A\of{v}} \int_{A\of{v}} C\of{\vec{x}} \func{d}A\]

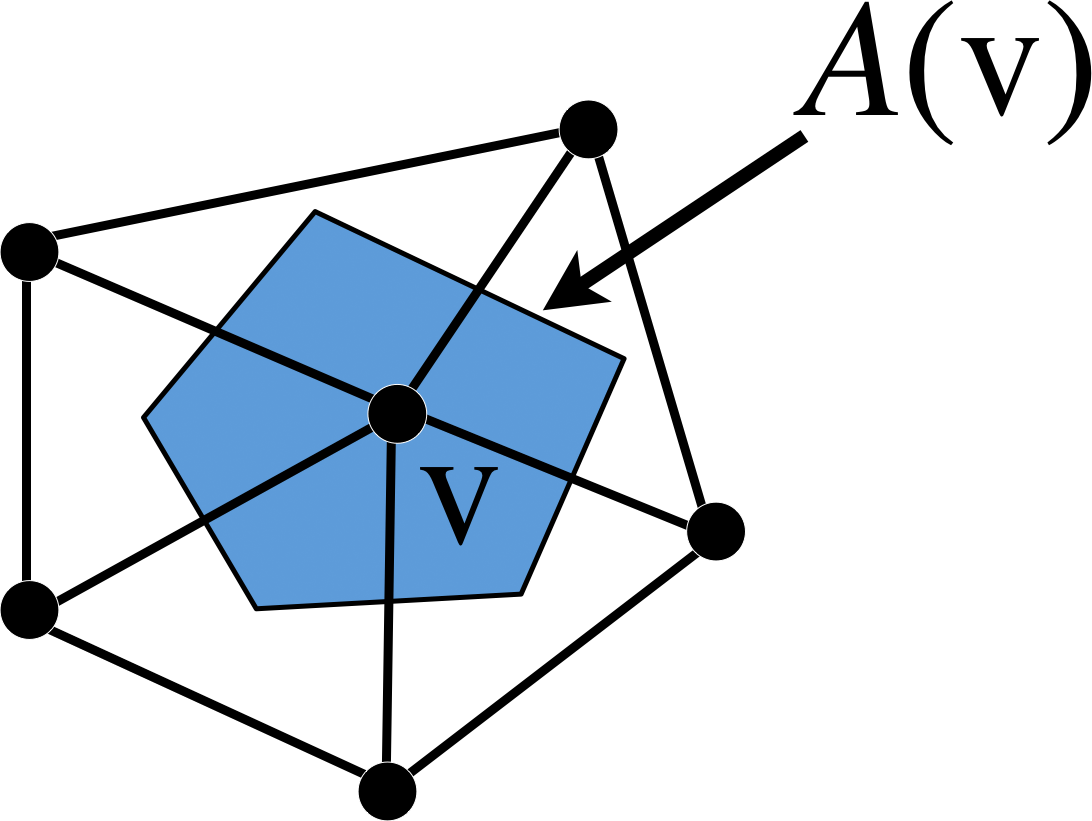
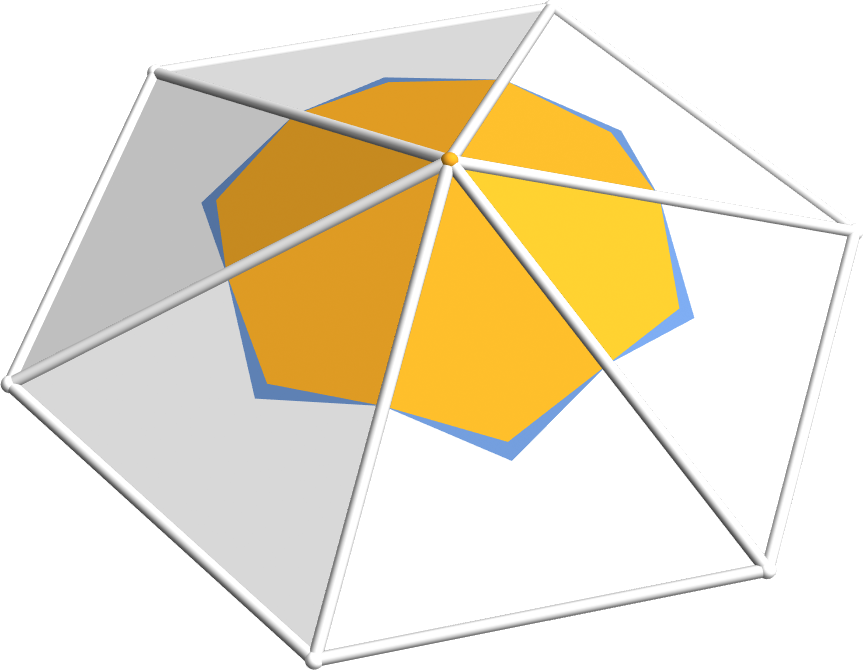
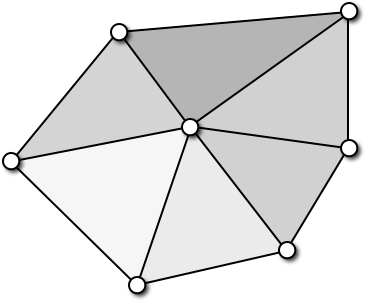
Barycentric Cells

For each triangle of one-ring, connect vertex with edge midpoints and triangle barycenters

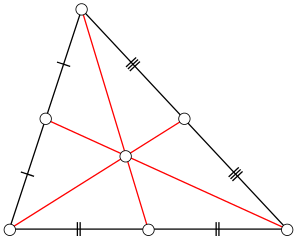
Simple to compute: Area is 1/3 of triangle areas
- How to compute triangle areas?

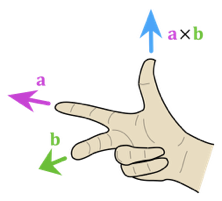
3D Cross Product

Given two 3D vectors \(\vec{a}\) and \(\vec{b}\), computes a vector \(\vec{c}\) that is orthogonal to them \[ \vec{c} \;=\; \vec{a} \times \vec{b} \;=\; {\tiny \matrix{ a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 }} \]

Measures the area of parallelogram spanned by vectors \(\vec{a}\) and \(\vec{b}\) \[ \norm{\vec{a} \times \vec{b}} = \norm{\vec{a}} \cdot \norm{\vec{b}} \cdot \sin\theta \]

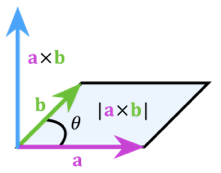
Measures volume spanned by vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) \[ \mathrm{vol}\of{\vec{a}, \vec{b}, \vec{c}} \;=\; \abs{ \vec{a} \, \vec{b} \, \vec{c} } \;=\; \trans{\left( \vec{a} \times \vec{b} \right)} \vec{c} \]

Wikipedia: Cross Product

Voronoi Cells

For each triangle of one-ring, connect vertex with edge midpoints and triangle circumcenter

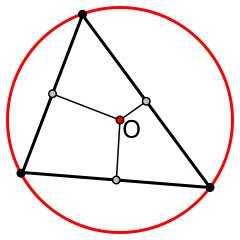
How to compute circumcircles? Intersection of perpendicular bisectors.

Barycentric vs. Voronoi Cells

Voronoi cells provide better approximation than barycentric cells, but are more complex to compute

barycentric

voronoi

comparison

comparison

Problem: Circumcenter can lie outside of triangle

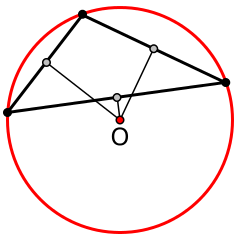
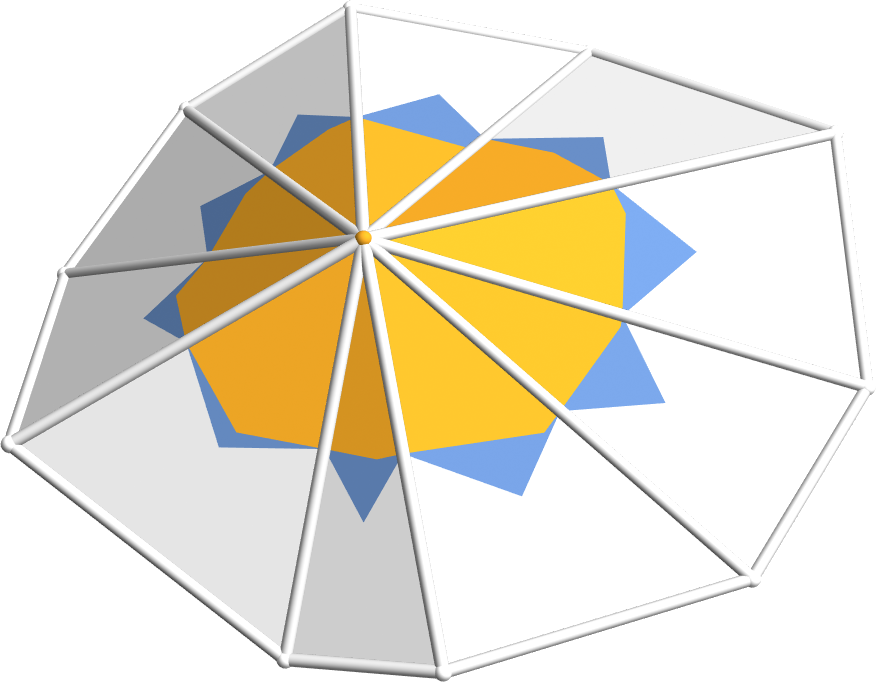
Mixed Cells

For each triangle of one-ring, connect vertex with edge midpoints and …
- … circumcenters for non-obtuse triangles
- … midpoints of opposite edge for obtuse triangles

See Meyer et al. 2003 for computational details.

Discrete Curvatures

How to discretize all the differential operators to triangle meshes?
- First derivative: gradients, tangents, normal
- Second derivative: Min, Max, Mean, and Gauss curvature
We do not want to directly discretize the second fundamental form, since second derivatives are hard to approximate for triangle meshes.

Discrete Curvatures

Compute Gaussian curvature \(K\):

-by discretizing Gauss-Bonnet Theorem
Compute mean curvature \(H\):

-by discretizing Laplace-Beltrami operator
Compute min and max curvatures:

-from \(H\) and \(K\) we can compute \(\kappa_1\) and \(\kappa_2\)

Gauss-Bonnet Theorem

Integral of Gaussian curvature over a surface \(\Omega\) and the geodesic curvature on its boundary \(\partial \Omega\) is a topological invariant
\[ \int_\Omega K \, dA + \int_{\partial \Omega} k_g \, ds = 2 \pi \, \chi(\Omega) \]
For \(\Omega\) with disk topology \(\chi(\Omega)=1\) and
\[ \int_\Omega K \, dA = 2 \pi - \int_{\partial \Omega} k_g \, ds\]

Wikipedia: Gauss-Bonnet Theorem

Discrete Gauss Curvature

Compute Gauss curvature by Gauss-Bonnet theorem and averaging
\[ K(v) \approx \frac{1}{| A(v) |} \int_{A(v)} K \, dA = \frac{1}{| A(v) |} \left( 2 \pi - \sum_j \theta_{j} \right)\]

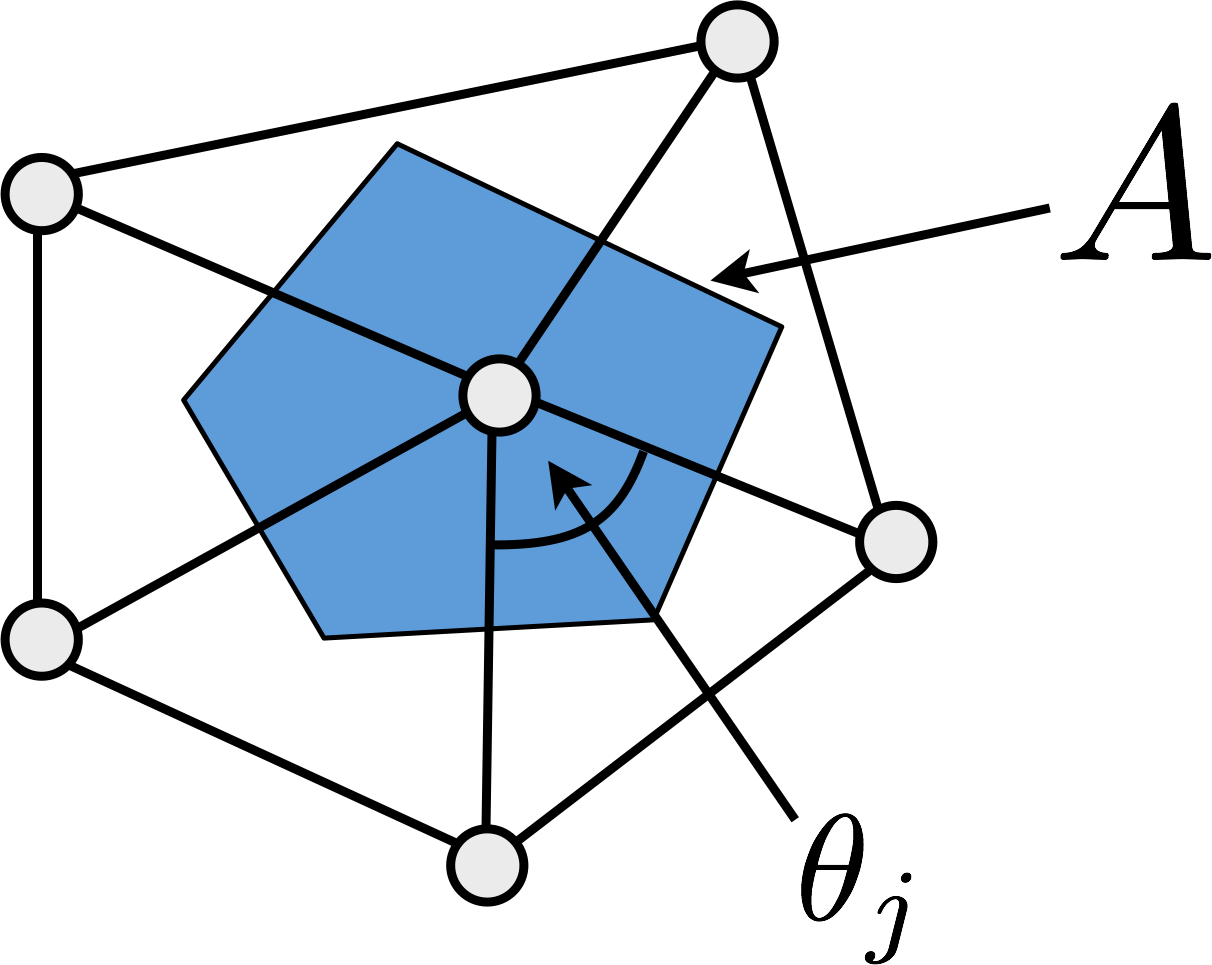
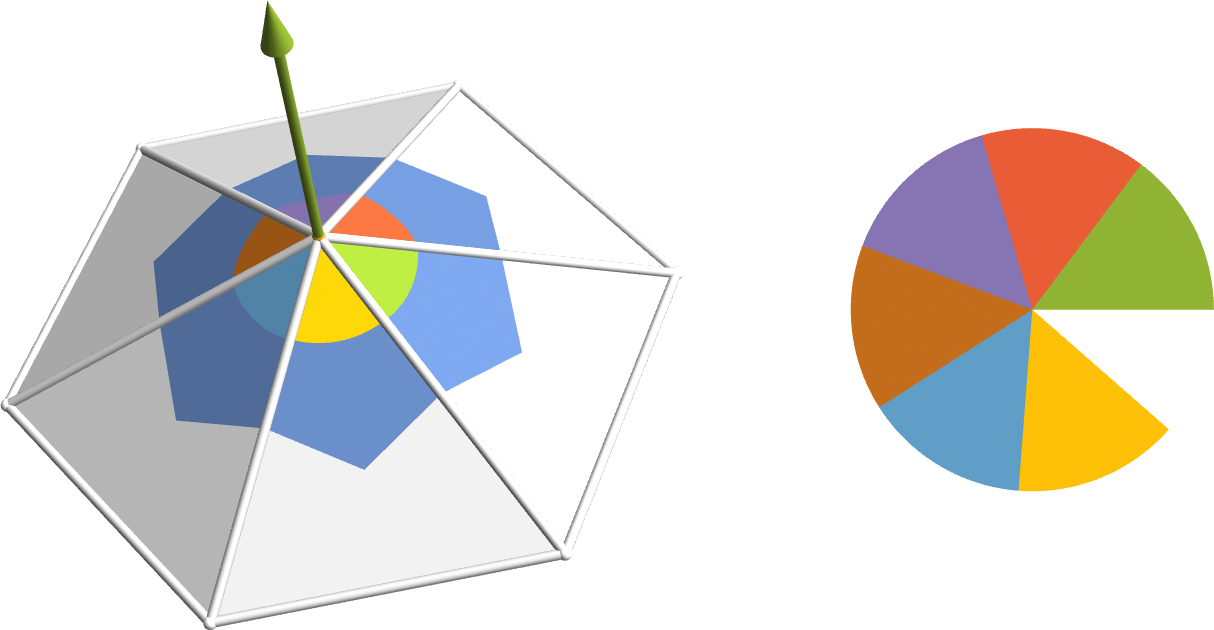
Discrete Gauss Curvature

Discrete Curvatures

Compute Gaussian curvature \(K\):

-by discretizing Gauss-Bonnet Theorem
Compute mean curvature \(H\):

-by discretizing Laplace-Beltrami operator
Compute min and max curvatures:

-from \(H\) and \(K\) we can compute \(\kappa_1\) and \(\kappa_2\)

Laplace Operator on Meshes?

Extend finite differences to meshes? Which weights to choose per vertex / edge?

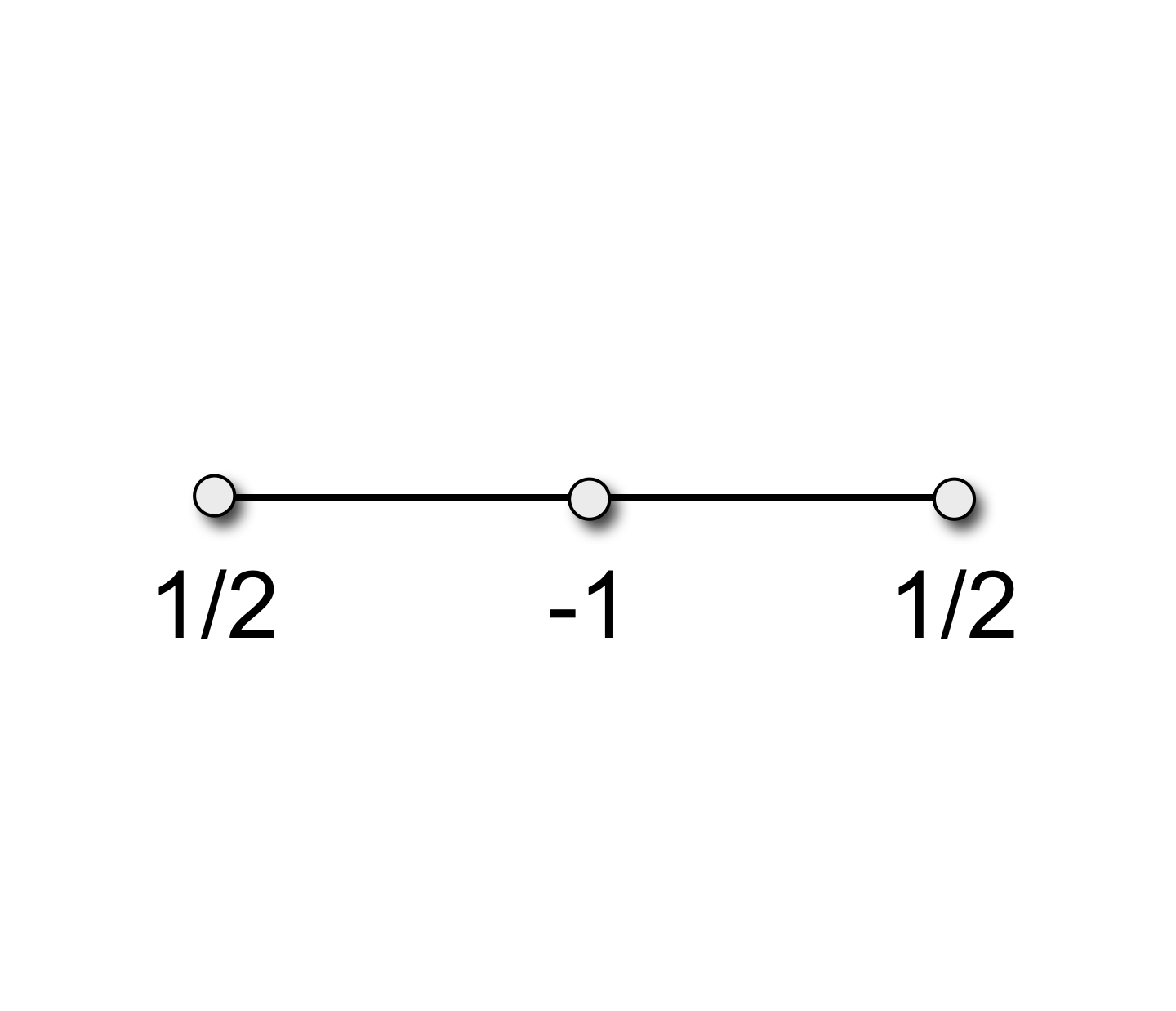
Uniform Laplace

Uniform Laplace-Beltrami discretization \[ \laplace_\func{uni} f\of{v_i} \;:=\; \frac{1}{\abs{\set{N}_1\of{v_i}}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( f\of{v_j} - f\of{v_i} \right) \]

Properties
- simple and efficient
- depends only on connectivity
- does not take into account geometry at all

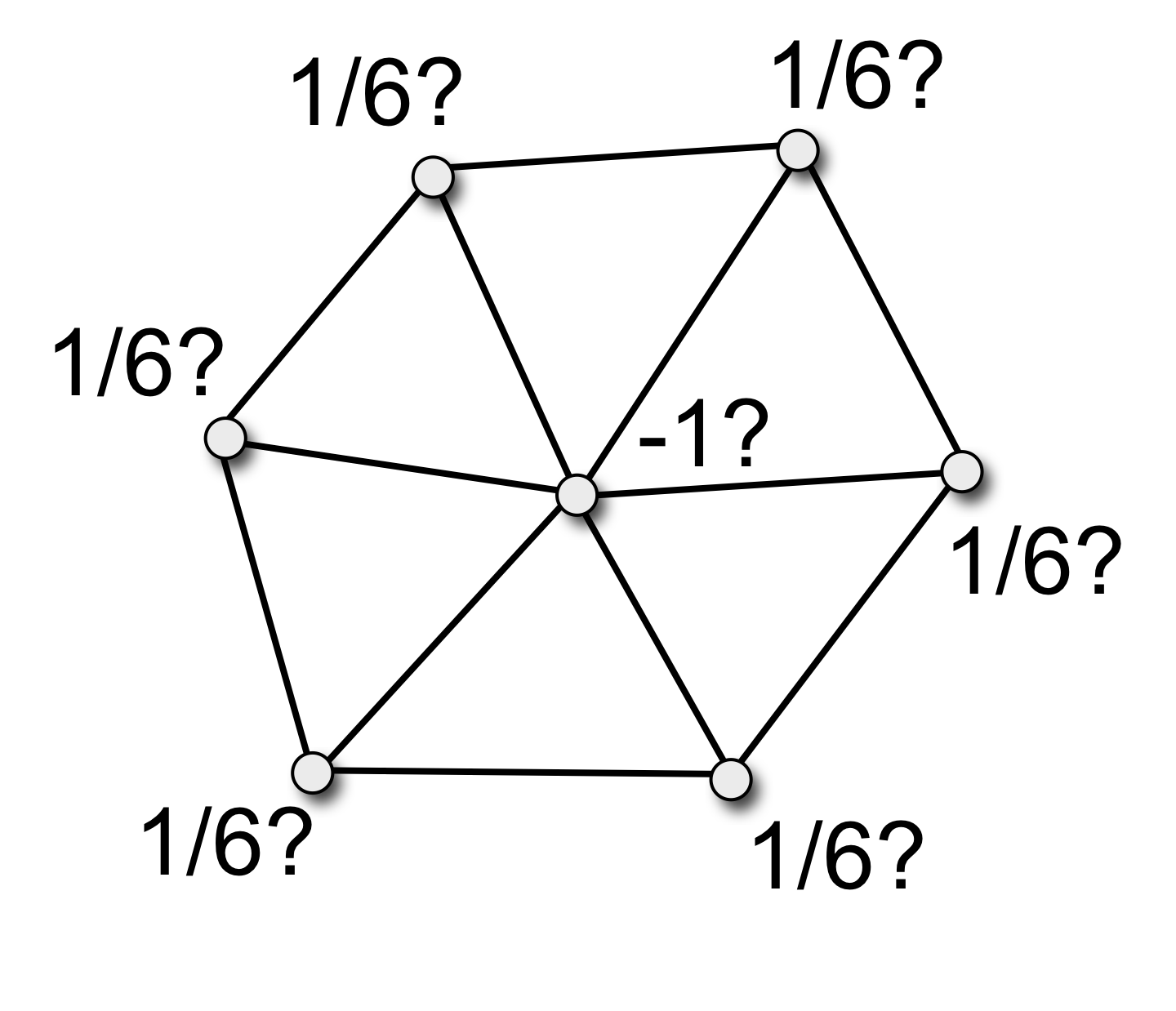
Uniform Laplace

Uniform Laplace-Beltrami discretization \[ \laplace_\func{uni} \vec{x}_i \;:=\; \frac{1}{\abs{\set{N}_1\of{v_i}}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \vec{x}_j - \vec{x}_i \right) \;\approx\; -2 H \vec{n} \]

Properties
- simple and efficient
- bad approximation for irregular triangulations, e.g. can give non-zero \(H\) for planar meshes
- does not take into account scale

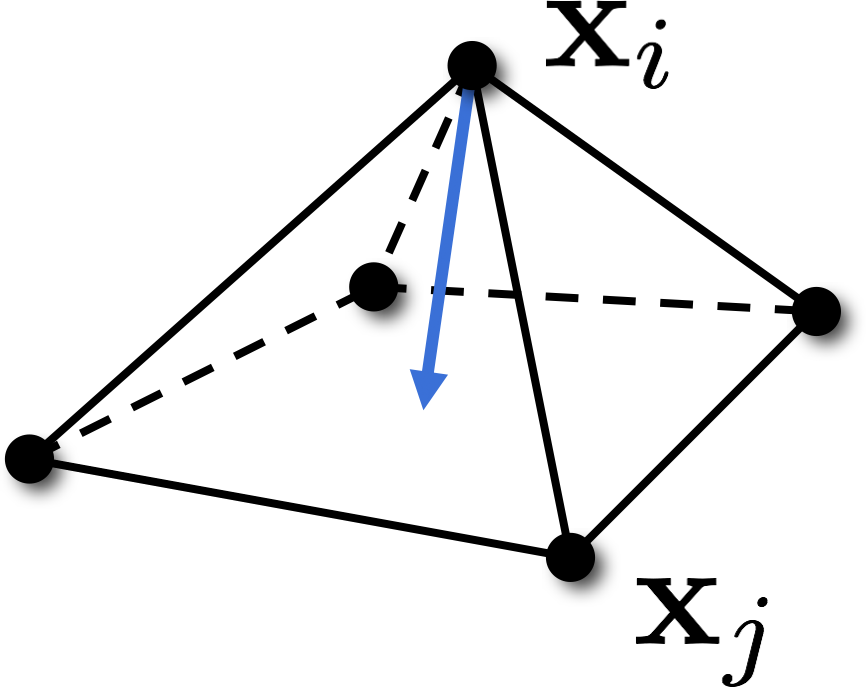
Divergence Theorem & Laplace

Divergence Theorem \[ \int_{A_i} \func{div} \, \vec{F} ( \vec{u} ) \mathrm{d}A = \int_{\partial A_i} \vec{F}(\vec{u}) \cdot \vec{n}(\vec{u}) \mathrm{d}s \]

Laplace operator \[ \int_{A_i} \Delta f(\vec{u}) \,\mathrm{d}A \;=\; \int_{A_i} \func{div} \grad f(\vec{u}) \,\mathrm{d}A \;=\; \int_{\partial A_i} \grad f(\vec{u}) \cdot \vec{n}(\vec{u}) \,\mathrm{d}s \]

Wikipedia: Divergence Theorem , Laplace Operator

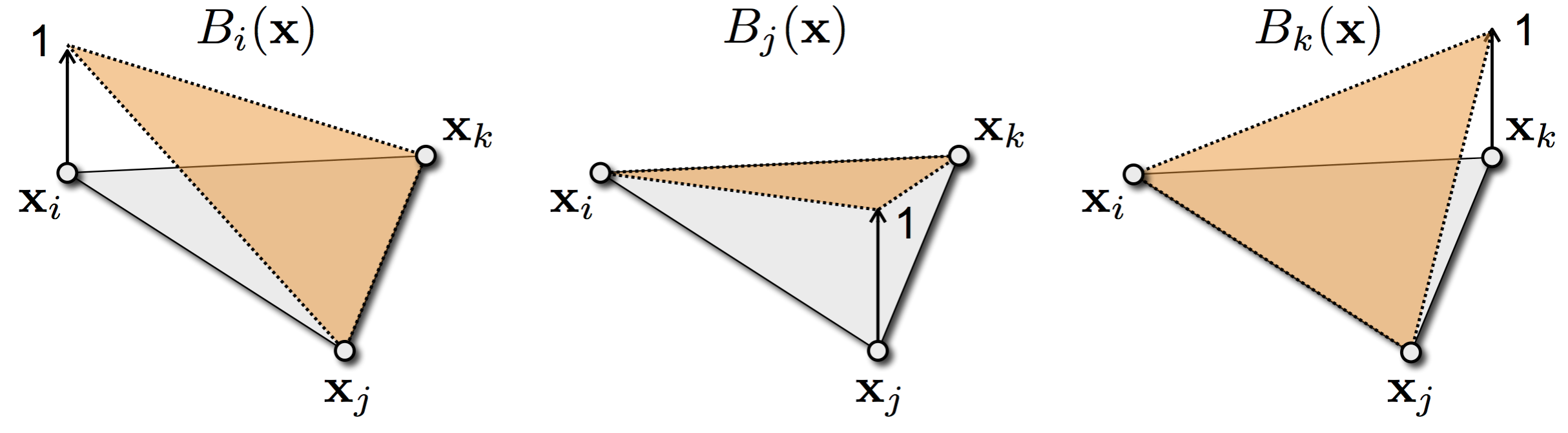
Functions on a Mesh

Given per-vertex values \(f(v_i) = f(\vec{x}_i) = f(\vec{u}_i) = f_i\) we obtain a piecewise linear function per triangle
\[f(\vec{u}) \;=\; f_i B_i (\vec{u}) + f_j B_j(\vec{u}) + f_k B_k(\vec{u})\]

We use linear basis functions \(B_i\), \(B_j\), \(B_k\) on a triangle

Gradients on a Mesh

The gradient of function \(f\) on triangle \((v_i, v_j, v_k)\) is \[ \grad f(\vec{u}) \;=\; f_i \grad B_i(\vec{u}) + f_j \grad B_j(\vec{u}) + f_k \grad B_k(\vec{u}) \]

Since \(B_i + B_j + B_k = 1\) we have \[ \grad B_i + \grad B_j + \grad B_k = 0 \]

Combining the two equations gives \[ \grad f(\vec{u}) \;=\; \left( f_j - f_i \right) \grad B_j(\vec{u}) + \left( f_k - f_i \right) \grad B_k(\vec{u}) \]

Wikipedia: Gradient

Gradients on a Mesh

The gradient of the linear basis functions \(B_i\), \(B_j\), \(B_k\) is \[ \grad B_i (\vec{u}) \;=\; \frac{ \left( \vec{x}_k - \vec{x}_j \right)^{\perp} }{ 2 \, A_T } \,,\quad \grad B_j (\vec{u}) \;=\; \frac{ \left( \vec{x}_i - \vec{x}_k \right)^{\perp} }{ 2 \, A_T } \,,\quad \grad B_k (\vec{u}) \;=\; \frac{ \left( \vec{x}_j - \vec{x}_i \right)^{\perp} }{ 2 \, A_T } \]

Combining with equations from previous slide we get \[ \grad f(\vec{u}) \;=\; \left( f_j - f_i \right) \frac{ \left( \vec{x}_i - \vec{x}_k \right)^{\perp} }{ 2 \, A_T } + \left( f_k - f_i \right) \frac{ \left( \vec{x}_j - \vec{x}_i \right)^{\perp} }{ 2 \, A_T } \]

Divergence Theorem & Laplace

Laplace operator \[ \int_{A_i} \Delta f(\vec{u}) \,\mathrm{d}A \;=\; \int_{\partial A_i} \grad f(\vec{u}) \cdot \vec{n}(\vec{u}) \,\mathrm{d}s \]

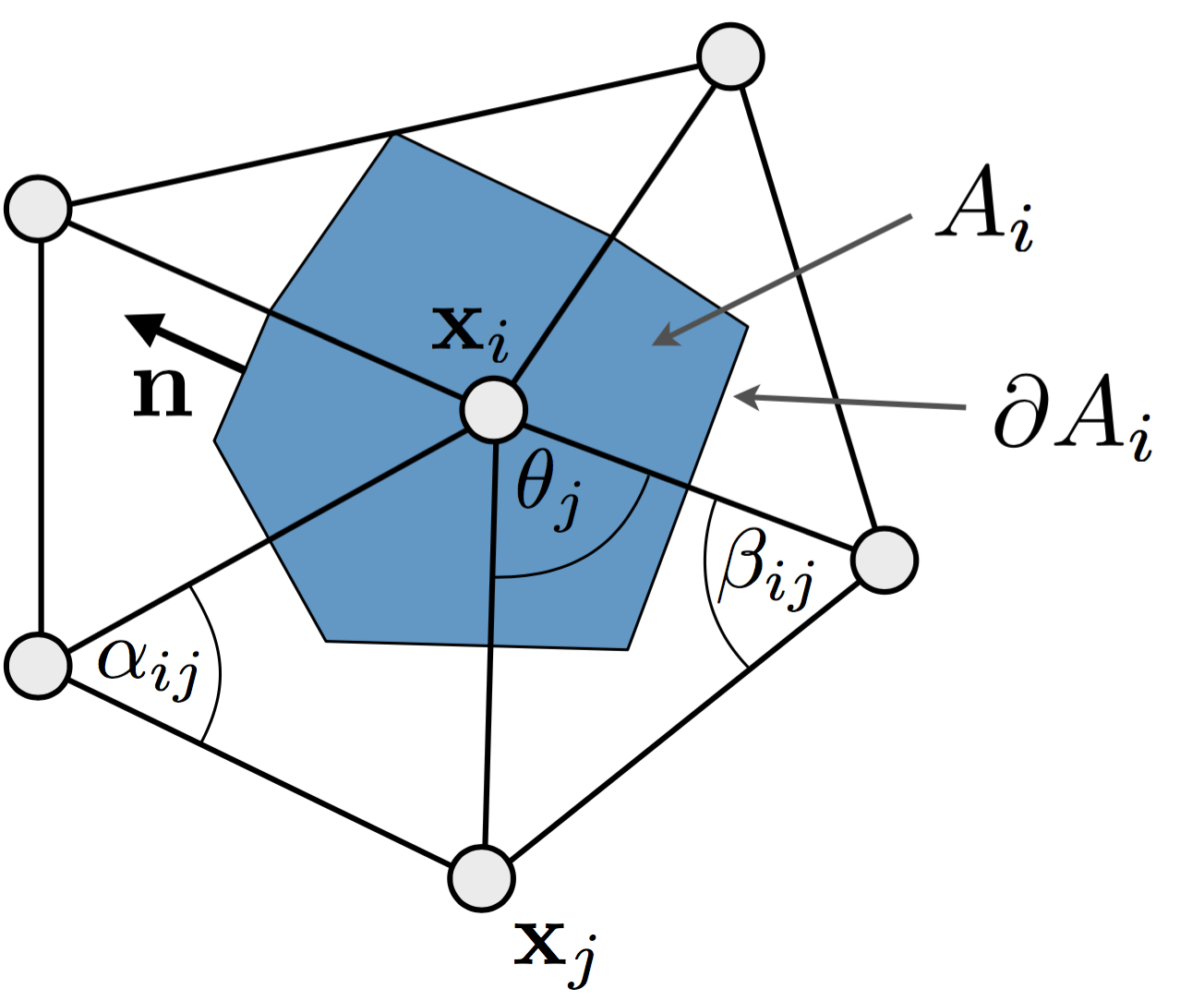
Per triangle segment \[ \begin{align} \int_{\partial A_i \cap T} \grad f(\vec{u}) \cdot \vec{n}(\vec{u}) \mathrm{d}s & \;=\; \grad f(\vec{u}) \cdot (\vec{a} - \vec{b})^{\perp} \\ & \;=\; \frac{1}{2} \grad f(\vec{u}) \cdot (\vec{x}_j - \vec{x}_k)^{\perp} \end{align} \]

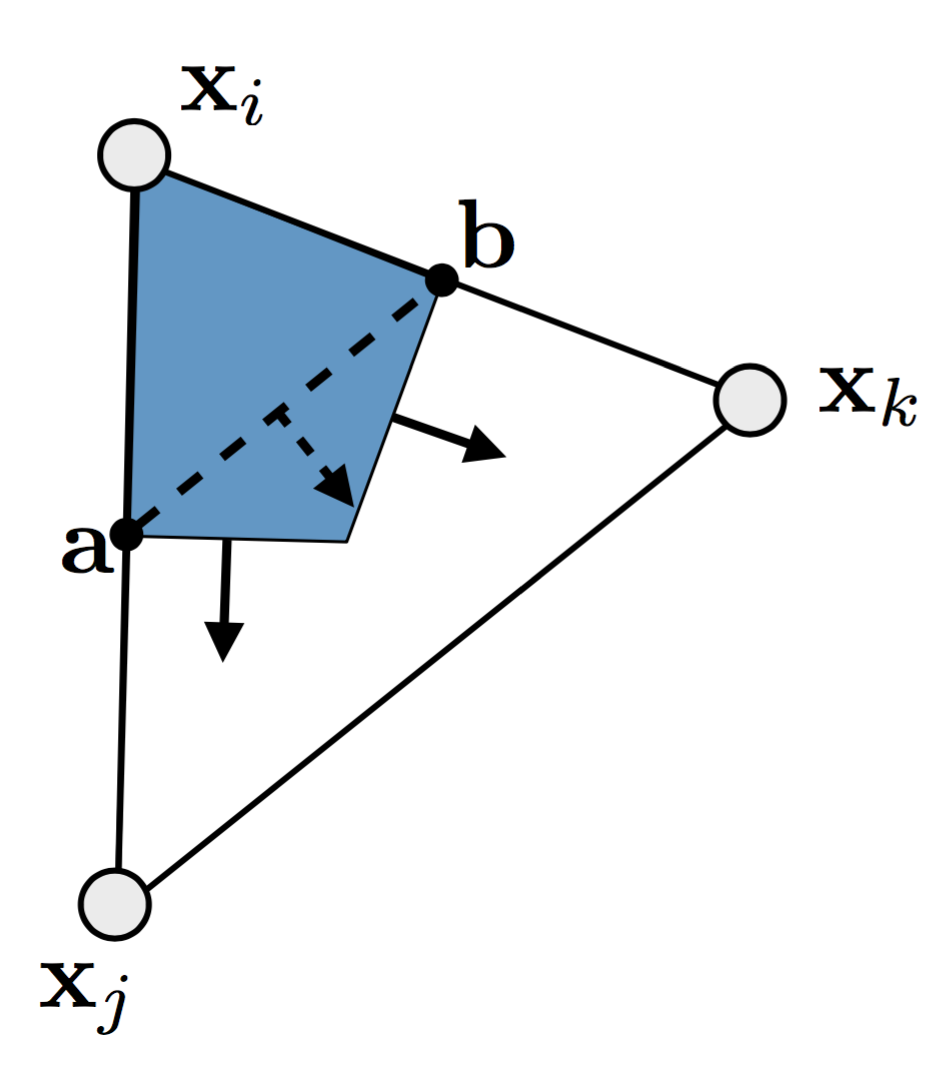
Discrete Laplace-Beltrami

\[ \begin{align*} \int_{\partial A_i \cap T} \grad f(\vec{u}) \cdot \vec{n}(\vec{u}) \mathrm{d}s & \;=\; \frac{1}{2} \grad f(\vec{u}) \cdot (\vec{x}_j - \vec{x}_k)^{\perp} \\ & \;=\; \begin{split}\left(f_j-f_i \right) \frac{\left(\vec{x}_i-\vec{x}_k \right)^{\perp} \cdot \left(\vec{x}_j-\vec{x}_k \right)^{\perp}}{4 A_T} \\ \;+\; \left(f_k-f_i \right) \frac{\left(\vec{x}_j-\vec{x}_i \right)^{\perp} \cdot \left(\vec{x}_j-\vec{x}_k \right)^{\perp}}{4 A_T}\end{split}\\ & \;\;\vdots\; \\ & \;=\; \frac{1}{2} \cot \gamma_k \left(f_j - f_i \right) \;+\; \frac{1}{2} \cot \gamma_j \left(f_k - f_i \right) \end{align*} \]

Discrete Laplace-Beltrami

Cotangent discretization
\[ \laplace_{\set{S}} f\of{v_i} \;:=\; \frac{1}{2A\of{v_i}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \cot \alpha_{ij} + \cot \beta_{ij} \right) \left( f\of{v_j} - f\of{v_i} \right)\]

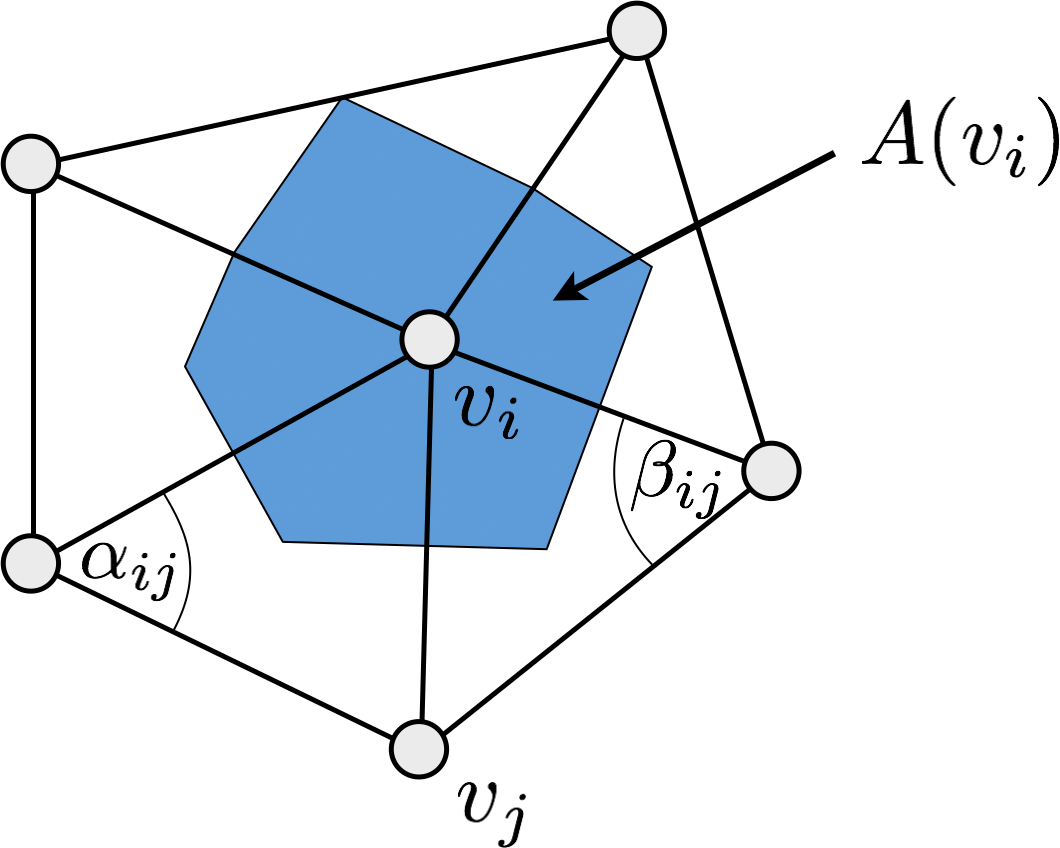
For a full derivation see Chapter 3.3.4 of PMP book

Discrete Laplace-Beltrami

Cotangent discretization
\[ \laplace_{\set{S}} f\of{v_i} \;:=\; \frac{1}{2A\of{v_i}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \cot \alpha_{ij} + \cot \beta_{ij} \right) \left( f\of{v_j} - f\of{v_i} \right)\]
Problems
- how to compute cotan?
- weights can become negative (when?)
- depends on triangulation
Still the most widely used discretization

Discrete Curvatures

Compute Gaussian curvature \(K\):

-by discretizing Gauss-Bonnet Theorem
Compute mean curvature \(H\):

-by discretizing Laplace-Beltrami operator
Compute min and max curvatures:

-from \(H\) and \(K\) we can compute \(\kappa_1\) and \(\kappa_2\)

Discrete Curvatures

Mean curvature (absolute value) \[ H(v_i) = \frac{1}{2} \norm{ \laplace_\set{S} \vec{x}_i}\]
Gaussian curvature \[ K(v_i) = (2 \pi - \sum_j \theta_{j}) \,/\, A(v_i) \]
Principal curvatures \[ \begin{eqnarray} \kappa_1(v_i) &=& H(v_i) + \sqrt {H(v_i)^2 - K(v_i)} \\ \kappa_2(v_i) &=& H(v_i) - \sqrt {H(v_i)^2 - K(v_i)} \end{eqnarray} \]

Discrete Mean & Principal Curvatures

Outlook

In the following lectures, the Laplacian will also be used to
- improve mesh quality
- compute a parameterization
- deform a surface
- etc.

The Laplacian is the central concept in this course!

Literature

Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 3

- Meyer et al.: Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. In Visualization and Mathematics III, Springer, 2003.

Title

Triangle Meshes

Why Triangle Meshes?

Why Triangle Meshes?

Why Triangle Meshes?

Why Triangle Meshes?

Why Triangle Meshes?

Mathematical Manifold Definition

Two-Manifold Surfaces

Mesh Data Structures

2D Mesh Combinatorics: Euler’s Polyhedron Formula

Face Set

Indexed Face Set

Face-Based Connectivity

Edge-Based Connectivity

Halfedge-Based Connectivity

One-Ring Traversal

Half-Edge navigation demo

Halfedge-Based Libraries

Triangle Meshes

Normal Vectors

Vertex Normals

Discrete Curvatures

Discrete Curvatures

Barycentric Cells

3D Cross Product

Voronoi Cells

Barycentric vs. Voronoi Cells

Mixed Cells

Discrete Curvatures

Discrete Curvatures

Gauss-Bonnet Theorem

Discrete Gauss Curvature

Discrete Gauss Curvature

Discrete Curvatures

Laplace Operator on Meshes?

Uniform Laplace

Uniform Laplace

Divergence Theorem & Laplace

Functions on a Mesh

Gradients on a Mesh

Gradients on a Mesh

Divergence Theorem & Laplace

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Discrete Curvatures

Discrete Curvatures

Discrete Mean & Principal Curvatures

Outlook

Literature