Geometry Processing

Smoothing

Prof. Edward Chien

Computer Graphics & Geometry Processing

Recall: Discrete Differential Geometry

Uniform Laplace

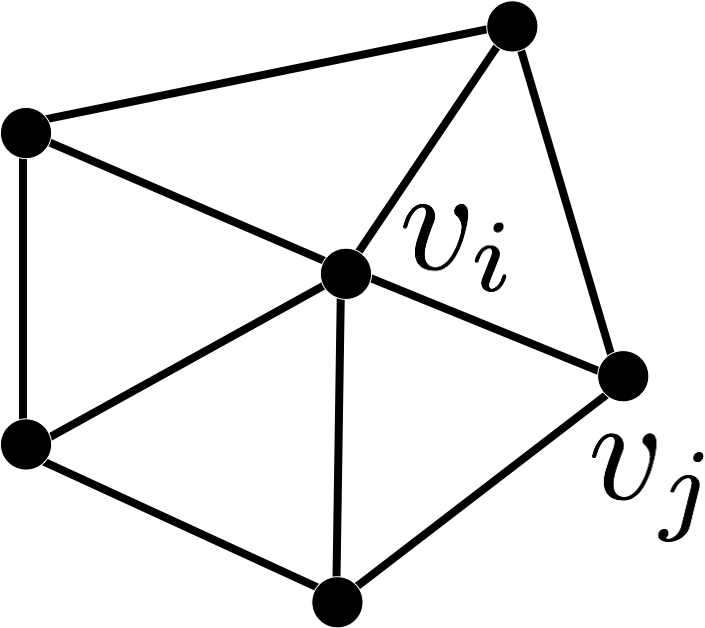
Uniform Laplace-Beltrami discretization \[ \laplace f\of{v_i} \;:=\; \frac{1}{\abs{\set{N}_1\of{v_i}}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( f\of{v_j} - f\of{v_i} \right) \]

Properties
- depends only on connectivity
- does not take into account geometry at all
- not accurate for irregular triangulations

Discrete Laplace-Beltrami

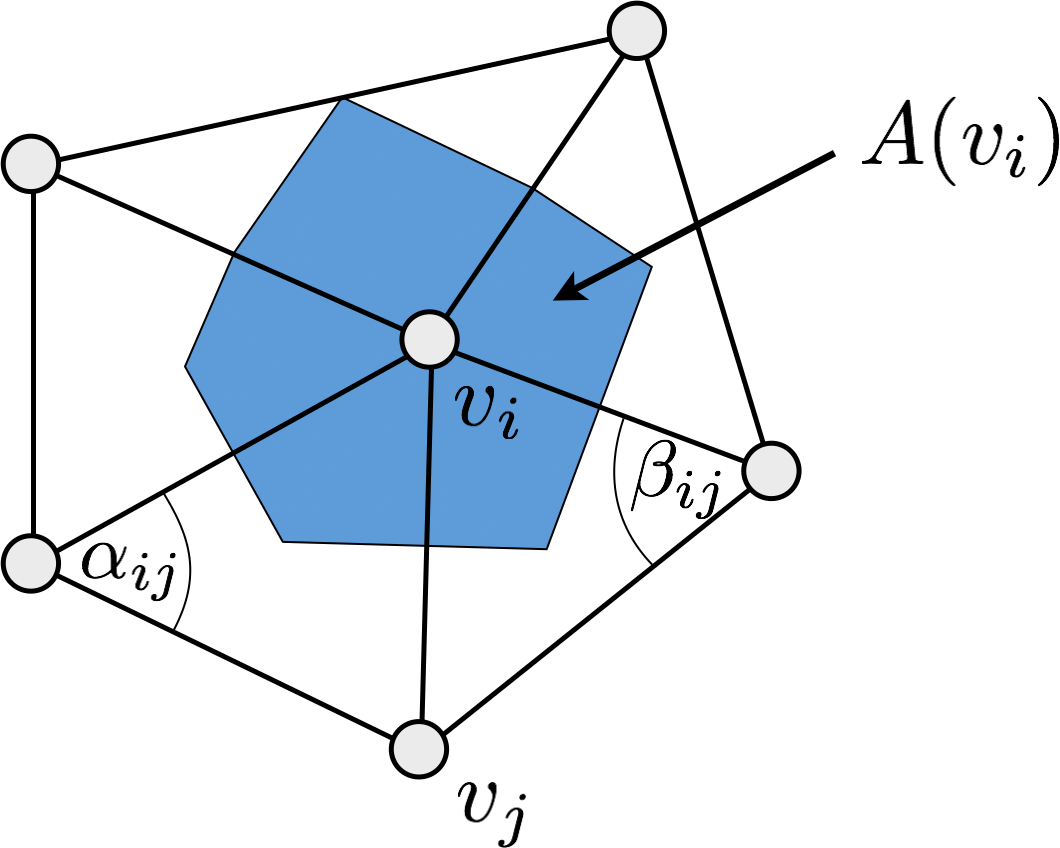
Cotangent Laplace-Beltrami discretization \[ \laplace_{\set{S}} f\of{v_i} \;:=\; \frac{1}{2A\of{v_i}} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \cot \alpha_{ij} + \cot \beta_{ij} \right) \left( f\of{v_j} - f\of{v_i} \right)\]

Properties
- depends on connectivity and geometry
- more accurate than uniform discretization
- weights can become negative
- most frequently used discretization

Discrete Curvatures

Mean curvature (absolute value) \[ H(v_i) = \frac{1}{2} \norm{ \laplace_\set{S} \vec{x}_i}\]
Gaussian curvature \[ K(v_i) = (2 \pi - \sum_j \theta_{j}) \,/\, A(v_i) \]
Principal curvatures \[ \begin{eqnarray} \kappa_1(v_i) &=& H(v_i) + \sqrt {H(v_i)^2 - K(v_i)} \\ \kappa_2(v_i) &=& H(v_i) - \sqrt {H(v_i)^2 - K(v_i)} \end{eqnarray} \]

Today: Mesh Smoothing

Motivation

Filter out high-frequency noise

Motivation

Filter out high-frequency noise

Desbrun et al.: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Motivation

Advanced filtering

Kim, Rosignac: Geofilter: Geometric Selection of Mesh Filter Parameters, Eurographics 2005

Outline

Spectral Analysis
Diffusion Equation
Numerical Solutions

Spectral Analysis

Fourier Transform

Represent a function as a weighted sum of sine and cosine functions

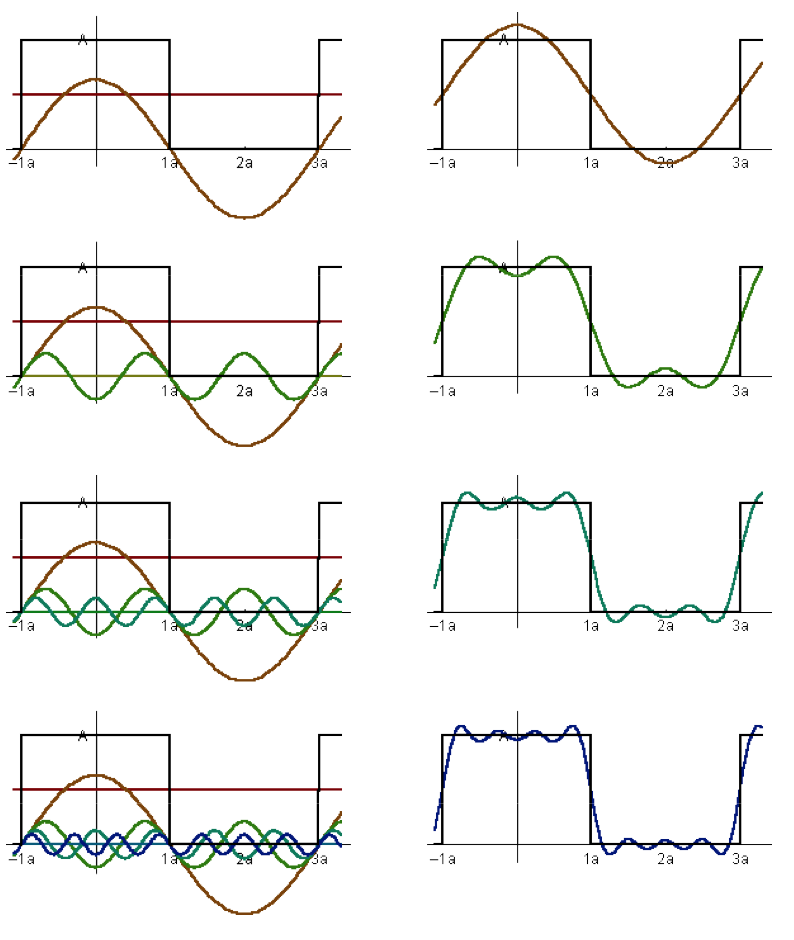
\[ f\of{x} \;=\; a_0 + a_1 \cos\of{x} + a_2 \cos\of{3x} + a_3 \cos\of{5x} + a_4 \cos\of{7x} + \dots \]

Fourier Transform

\[F(\omega) = \int_{-\infty}^{\infty} f(x) \, \func{e}^{-2\pi\func{i}\omega x} \func{d}x\]

\[f(x) = \int_{-\infty}^{\infty} F(\omega) \, \func{e}^{2\pi\func{i}\omega x} \;\func{d}\omega\]

Wikipedia: Fourier Transform and \(L^2\) Inner Product

Convolution

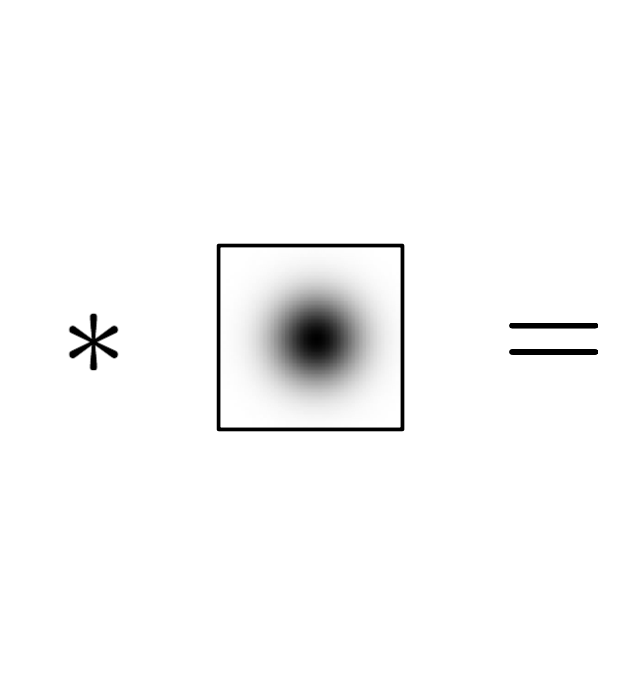
Smooth signal by convolution with a kernel function \[ h(x) \;=\; f * g \;:=\; \int f(y) \cdot g(x-y) \,\func{d}y \]
Example: Gaussian blurring

Wikipedia: Convolution

Convolution

Smooth signal by convolution with a kernel function \[ h(x) \;=\; f * g \;:=\; \int f(y) \cdot g(x-y) \,\func{d}y \]
Convolution in spatial domain ⇔ Multiplication in frequency domain \[ H\of{\omega} \;=\; F\of{\omega} \cdot G\of{\omega} \]

Filtering with Fourier Transform

Spatial domain \(f(x) \rightarrow\) frequency domain \(F(\omega)\)
\[ F(\omega) = \int_{-\infty}^{\infty} f(x) \, \func{e}^{-2\pi \func{i}\omega x} dx\]
Multiply by low-pass filter \(G(\omega)\)
\[ \tilde{F}(\omega) = F(\omega) G(\omega)\]
Frequency domain \(\tilde{F}(\omega) \rightarrow\) spatial domain \(\tilde{f}(x)\)
\[ \tilde{f}(x) = \int_{-\infty}^{\infty} \tilde{F}(\omega) \, \func{e}^{2\pi \func{i}\omega x} dx\]

Filtering with Fourier Transform

Filtering with Fourier Transform

Spectral Analysis for Meshes

Fourier transform requires functional representation
How to generalize to meshes?
Observation: Complex waves are eigenfunctions of Laplacian \[\Delta e^{2 \pi \func{i} \omega x} = \frac{\func{d}^2}{\func{d}x^2} \func{e}^{2 \pi \func{i} \omega x} = -(2 \pi \omega)^2 \func{e}^{2 \pi \func{i} \omega x}\]
Idea: Use eigenfunctions of discrete Laplace-Beltrami as spectral basis

Wikipedia: Eigenfunctions

Discrete Laplace-Beltrami

Function values sampled at the \(n\) mesh vertices \[\vec{f} = [f(v_1), f(v_2), \ldots, f(v_n)]\T \in \R^n\]
Discrete Laplace-Beltrami (per vertex) \[ \laplace f\of{v_i} = \frac{1}{2A_i} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \func{cot} \alpha_{ij} + \func{cot} \beta_{ij} \right) \left( f \of{v_j} - f \of{v_i} \right)\]

Discrete Laplace-Beltrami

Discrete Laplace operator is sparse matrix \(\mat{L} = \mat{DM} \in \R^{n \times n}\)

\[ \matrix{\vdots \\ \laplace_\set{S} f\of{v_i} \\ \vdots} \;=\; \mat{L} \cdot \matrix{\vdots \\ f \of{v_i} \\ \vdots} \]

Discrete Laplace-Beltrami

Discrete Laplace operator is sparse matrix \(\mat{L} = \mat{DM} \in \R^{n \times n}\)

\[ \begin{align} \mat{M}_{ij} \;&=\; \begin{cases} \func{cot}\alpha_{ij} + \func{cot}\beta_{ij}, & i \ne j \,,\; j \in \set{N}_1\of{v_i} \\ - \sum_{v_j \in \set{N}_1 \of{v_i}}\of{ \func{cot}\alpha_{ij} + \func{cot}\beta_{ij} } & i=j \\ 0 & \text{otherwise} \end{cases} \\[2mm] \mat{D} \;&=\; \func{diag}\of{ \dots, \frac{1}{2A_i}, \dots} \end{align} \]

Spectral Mesh Analysis

Discrete Laplace operator is sparse matrix \(\mat{L} = \mat{DM} \in \R^{n \times n}\)
- Eigenvectors are “natural vibrations”
- Eigenvalues are “natural frequencies”

Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\)
Reconstruct mesh from those (component-wise) \[ \begin{align} \vec{x} &:= \left[ x_1, \dots, x_n \right] & \vec{y} &:= \left[ y_1, \dots, y_n \right] & \vec{z} &:= \left[ z_1, \dots, z_n \right] \\ \vec{x} &\leftarrow \sum_{i=1}^k \, \left( \trans{\vec{x}} \vec{e}_i \right) \vec{e}_i & \vec{y} &\leftarrow \sum_{i=1}^k \, \left( \trans{\vec{y}} \vec{e}_i \right) \vec{e}_i & \vec{z} &\leftarrow \sum_{i=1}^k \, \left( \trans{\vec{z}} \vec{e}_i \right) \vec{e}_i \end{align} \]

Math Background: Inner Product

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\)
Reconstruct mesh from those (component-wise)

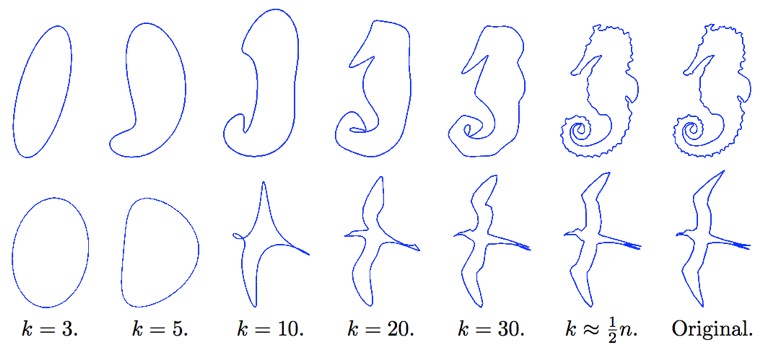
Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\) Too complex for large meshes 😢
Reconstruct mesh from those (component-wise)

Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Diffusion Flow

Diffusion equation is frequently used to smooth signals \[\frac{\partial f}{\partial t} = \lambda \Delta f\]
- \(\lambda\) is the diffusion constant
- \(\Delta\) is the Laplace operator
Solve numerically
- Discretize function in space & time
- Discretize time derivative
- Discretize spatial derivatives

Wikipedia: Diffusion Equation

Discretize PDE on Regular Grid

Sample function \(f(x,y,t)\) on a regular grid with spacing \(h\) and time-step \(\delta_t\) \[f[i,j,t] \;=\; f\left(i \cdot h, j \cdot h, t \cdot \delta t \right) \]

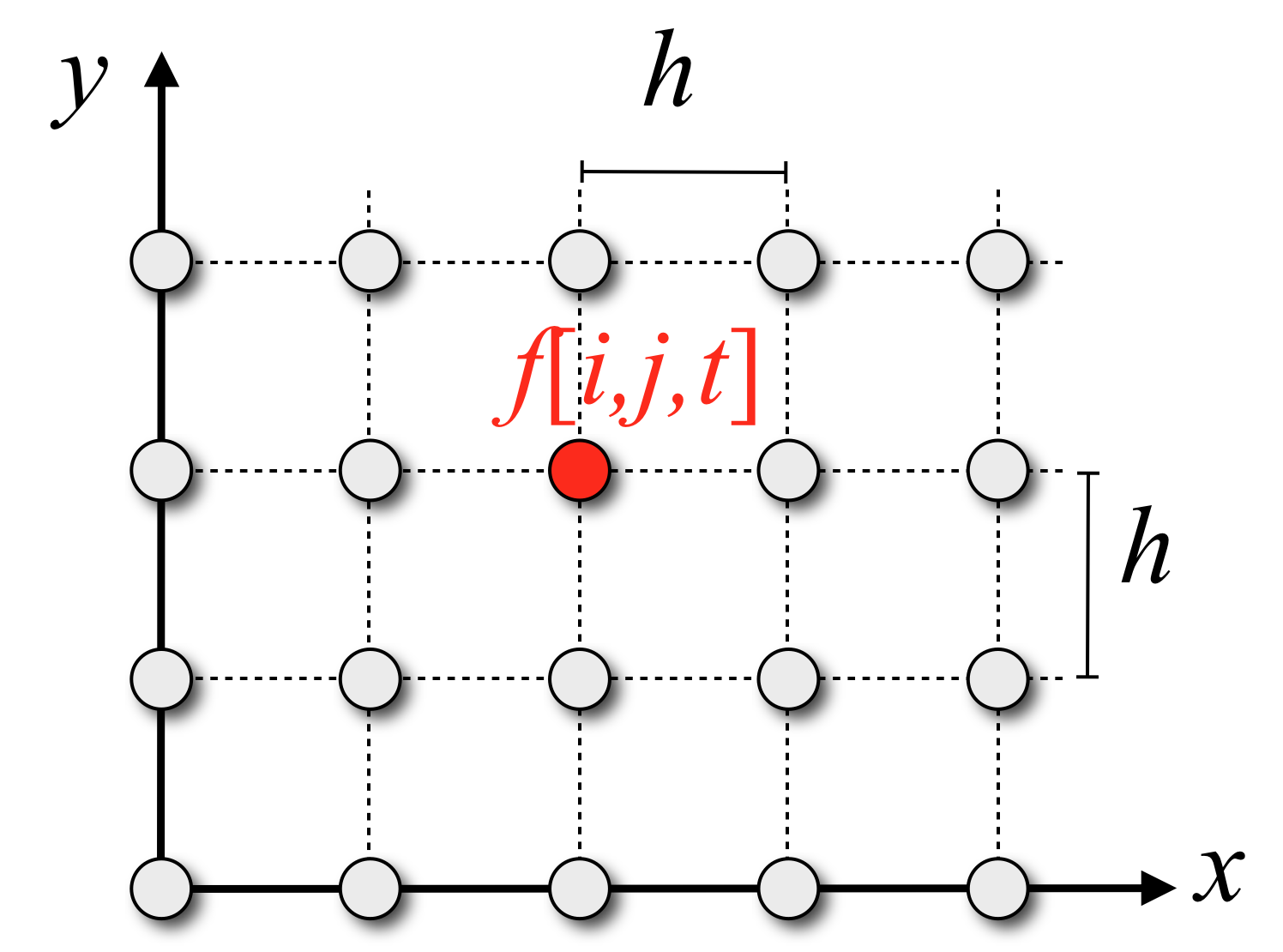
Discretize PDE on Regular Grid

Sample function \(f(x,y,t)\) on a regular grid with spacing \(h\) and time-step \(\delta_t\) \[f[i,j,t] \;=\; f\left(i \cdot h, j \cdot h, t \cdot \delta t \right) \]
Approximation of temporal derivative \[ f_{,t}[i,j,t] \;\approx\; \frac{f[i,j,t+1] - f[i,j,t]}{\delta t}\]
Approximation of Laplacian \[ \laplace f[i,j,t] \;=\; \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2} \]

Diffusion Flow in 2D

Continuous PDE \[f_{,t} \;=\; \lambda \left( f_{,xx} + f_{,yy} \right)\]
Finite difference discretization \[\frac{f[i,j,t+1] - f[i,j,t]}{\delta t} \;=\; \lambda \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2}\]
Leads to explict Euler time-integration \[f[i,j,t+1] \;=\; f[i,j,t] + \delta t \lambda \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2}\]
- \(\delta t \lambda\) has to be small for explicit Euler (<1 in this case)!

Diffusion in 2D

Diffusion Flow on Meshes

Continuous PDE: \(\frac{\partial \vec{x}}{\partial t} \;=\; \lambda \Delta \vec{x}\)
Discretization: \(\vec{x}_i \leftarrow \vec{x}_i + \delta t \, \lambda \Delta \vec{x}_i\)

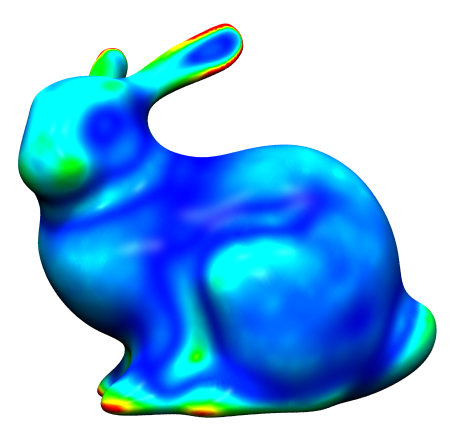
Diffusion Flow on Meshes

Problem: Time step needs to be very small to give stable results when using cotan Laplacian with area normalization
Better results with normalized weights (and ignoring the area term) \[\laplace \vec{x}_i \;=\; \frac{1}{\sum_{v_j \in \set{N}_1\of{v_i}} w_{ij}} \sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \left( \vec{x}_j - \vec{x}_i \right) \]
- Uniform weights \(w_{ij} = 1\)
- Cotangent weights \(w_{ij} = \cot\alpha_{ij} + \cot\beta_{ij}\)

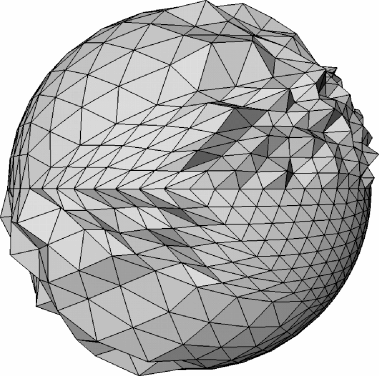
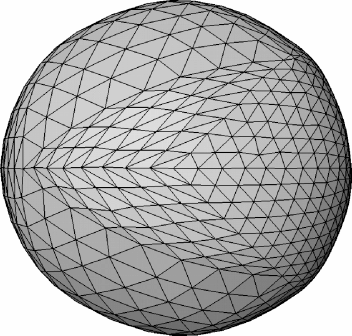
Uniform Laplace Discretization

Smoothes geometry and triangulation
Can be non-zero even for planar triangulations
Vertex drift can lead to distortions
Might be desired for mesh regularization

Desbrun et al.: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

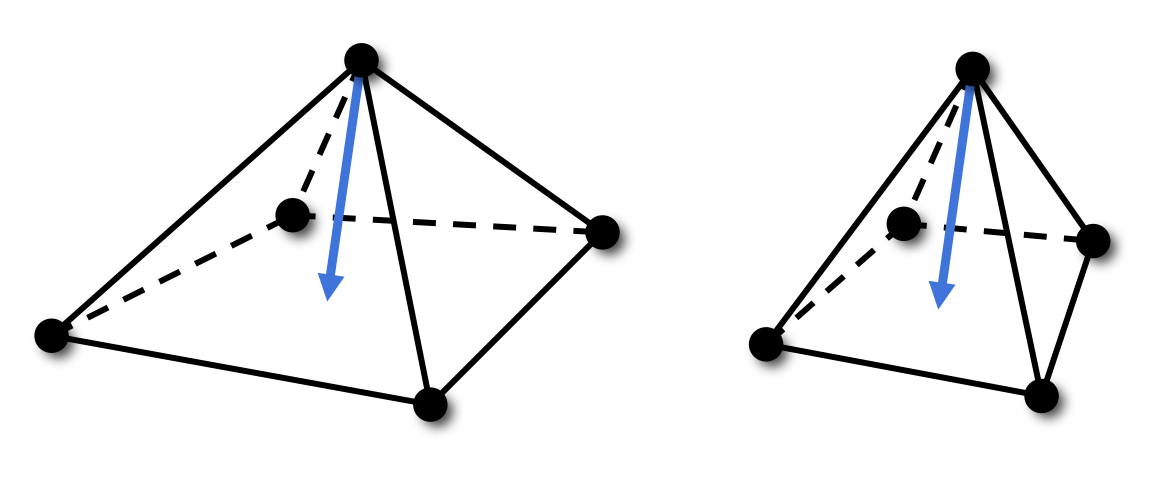
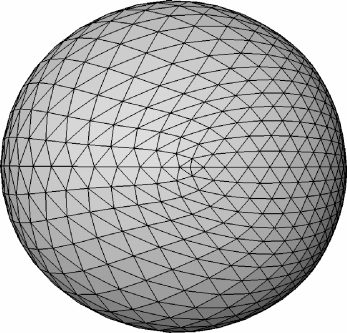
Uniform vs Cotan Discretization

Numerical Solutions

Numerical Integration

Let’s write the position update in matrix notation
Write all points \(\vec{x}_i^{(t)}\) in a large vector/matrix: \[\vec{X}^{(t)} = \trans{\left( \vec{x}_1^{(t)}, \ldots, \vec{x}_n^{(t)} \right)} \in \R^{n\times 3}\]
Matrix version of explicit integration (requires small \(\delta t \lambda\)) \[\vec{X}^{(t+1)} = (\vec{I} + \delta t \, \lambda \vec{L}) \, \vec{X}^{(t)}\]
Matrix version of implicit integration (works for any \(\delta t \lambda\)) \[(\vec{I} - \delta t \, \lambda \vec{L}) \, \vec{X}^{(t+1)} = \vec{X}^{(t)}\]

Wikipedia: Explicit/Implicit Integration

How to solve the linear system?

Solve linear system in each iteration \[(\vec{I} - \delta t \, \lambda \vec{L}) \vec{X}^{(t+1)} = \vec{X}^{(t)}\]
Matrix \(\vec{L} = \vec{DM}\) is built from Laplace weights \[\mat{M}_{ij} \;=\; \begin{cases} \func{cot}\alpha_{ij} + \func{cot}\beta_{ij}, & i \ne j \,,\; j \in \set{N}_1\of{v_i} \\ - \sum_{v_j \in \set{N}_1 \of{v_i}}\of{ \func{cot}\alpha_{ij} + \func{cot}\beta_{ij} } & i=j \\ 0 & \text{otherwise} \end{cases} \]

\[\mat{D} = \func{diag}\of{ \dots, \frac{1}{2A_i}, \dots}\]

How to solve the linear system?

Solve linear system in each iteration \[(\vec{I} - \delta t \, \lambda \vec{L}) \vec{X}^{(t+1)} = \vec{X}^{(t)}\]
Which solvers do you know?
- Gaussian elimination? 💣
- LU factorization? 💣
Analyze the properties of your system matrix!
- very sparse (about 7 non-zeros per row) 😄
- but not symmetric 😢

How to solve the linear system?

Matrix \(\vec{L} = \vec{DM}\) is not symmetric because of \(\vec{D}\).
Symmetrize it by multiplying with \(\vec{D}^{-1}\) from the left \[(\vec{D}^{-1} - \delta t \, \lambda \vec{M}) \vec{X}^{(t+1)} = \vec{D}^{-1} \vec{X}^{(t)}\]
Now the linear system is
- sparse 😄
- symmetric 😄
- positive definite 😄
We can use much more efficient solvers!
- conjugate gradients 😘
- sparse Cholesky factorization 😍

See Scientific Computing course notes

Try it yourself!

Literature

Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 4

Taubin, A Signal Processing Approach to Fair Surface Design, SIGGRAPH 1995
Desbrun, Meyer, Schröder, Barr, Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Title

Recall: Discrete Differential Geometry

Uniform Laplace

Discrete Laplace-Beltrami

Discrete Curvatures

Today: Mesh Smoothing

Motivation

Motivation

Motivation

Outline

Spectral Analysis

Fourier Transform

Fourier Transform

Convolution

Convolution

Filtering with Fourier Transform

Filtering with Fourier Transform

Filtering with Fourier Transform

Spectral Analysis for Meshes

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Spectral Mesh Analysis

Spectral Mesh Analysis

Spectral Mesh Analysis

Spectral Mesh Analysis

Diffusion Flow

Diffusion Flow

Discretize PDE on Regular Grid

Discretize PDE on Regular Grid

Diffusion Flow in 2D

Diffusion in 2D

Diffusion Flow on Meshes

Diffusion Flow on Meshes

Uniform Laplace Discretization

Uniform vs Cotan Discretization

Numerical Solutions

Numerical Integration

How to solve the linear system?

How to solve the linear system?

How to solve the linear system?

Try it yourself!

Literature