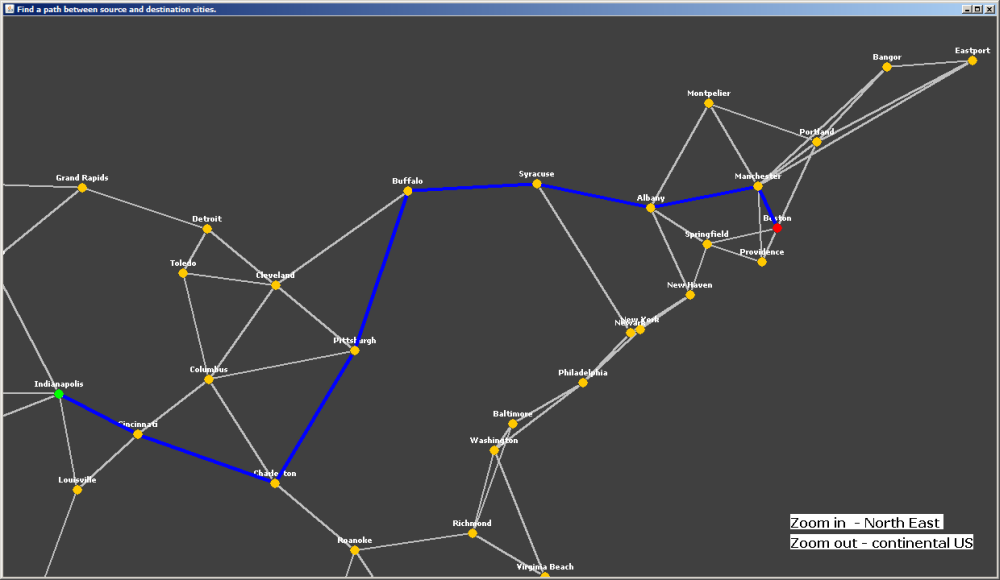
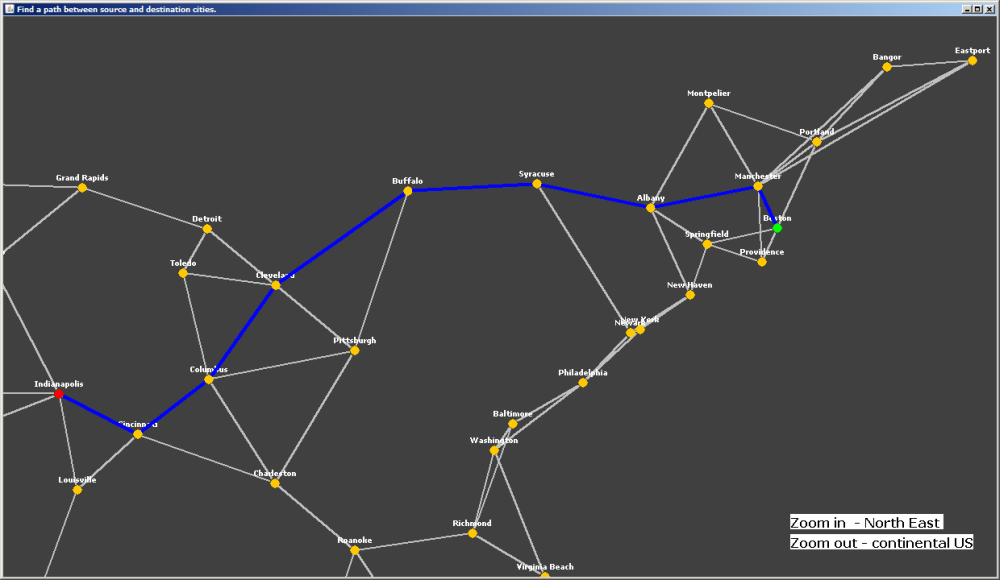
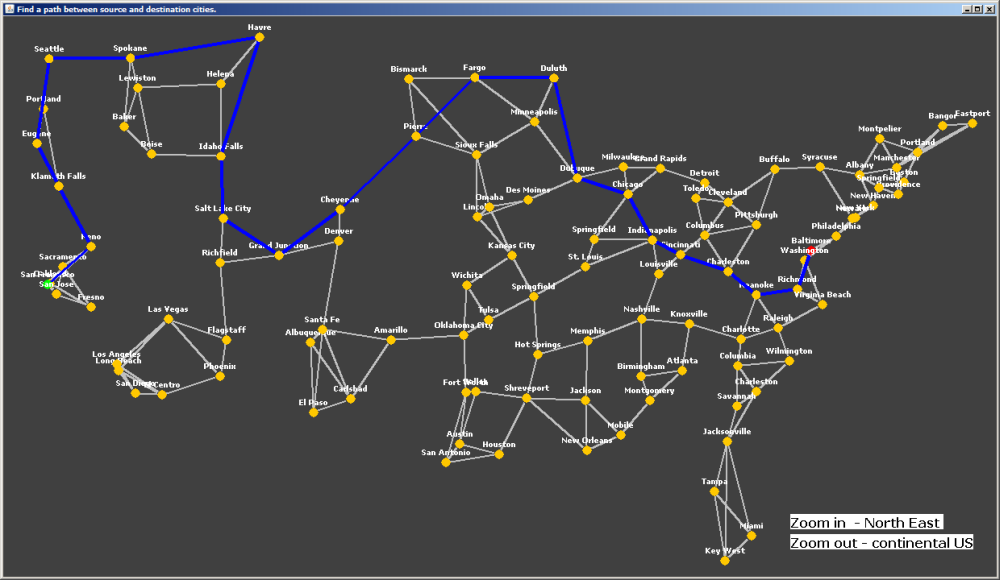
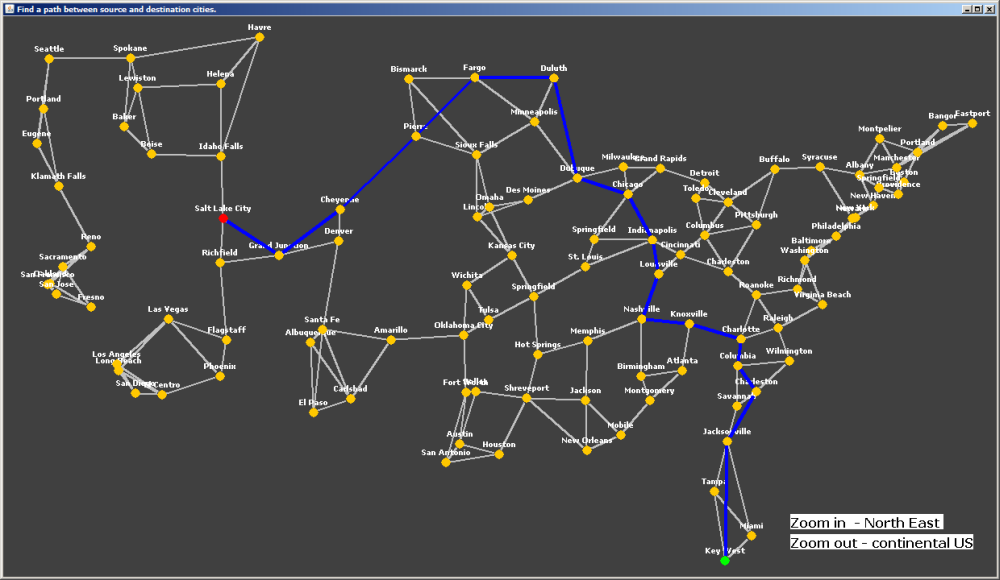
The Breadth First Search (BFS) traversal for graphs is very similar to level order traversal in trees and is briefly outlined below:
- Start BFS traversal from the source_node.
- Instead of children for a node in a tree, we have "neighbors" for a node in a graph.
The neighbors for node V are obtained from the row of adjacency_matrix A corresponding to V.
To get V's neighbors: find the cells A[V][0], A[V][1],..., A[V][num_cities - 1] that contain a "true" value.
- Use a queue like we did for level order traversal.
In each iteration remove a node V from the head of the queue and add V's not-visited neighbors (lets call the neighbor N_v) to the tail of the queue. Mark each of N_v as visited and set the previous node of N_v as V, this step is described in bullet (5) below.
If one of N_v is the the destination node, we are done.
Repeat this process until either we reach the destination node or the queue gets empty.
If the queue empties before we reach destination, this implies that the source and destination are disconnected in the graph.
- Keep track of nodes that are visited during the BFS traversal so that we do not revisit the same node (to avoid getting stuck in a cycle).
- For each visited node V_n: store the previous node P_n via which we visited V_n during BFS traversal.
This is similar to the parent node in trees, since there are no parent nodes in a graph the previous nodes are defined based on the traversal.
These previous nodes are needed to retrace our path to the source once we reach the destination node in
our BFS traversal.
|