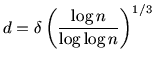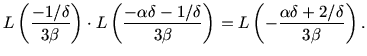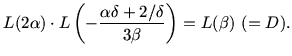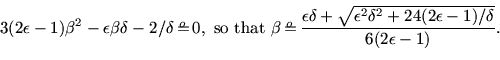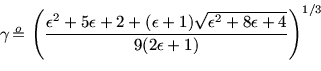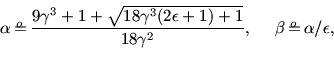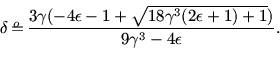

Next: The circuits for integer
Up: Analysis of Bernstein's Factorization
Previous: Introduction
Subsections
Background on the number field sieve
In theory and in practice the two main steps of the NFS
are the relation collection step
and the matrix step. We review their heuristic asymptotic runtime
analysis because it enables us to stress several points
that are important for a proper understanding of ``standard-NFS'' and
of ``circuit-NFS'' as proposed in [1].
2.1. Smoothness.
An integer is
called 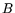 -smooth if all its prime factors are at most
-smooth if all its prime factors are at most 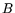 .
Following [10, 3.16]
we denote by
.
Following [10, 3.16]
we denote by
![$ L_x[r;\alpha]$](img8.png) any function of
any function of 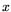 that equals
that equals
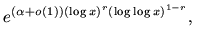 for
for 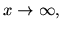
where 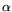 and
and 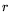 are real numbers with
are real numbers with
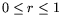 and
logarithms are natural. Thus,
and
logarithms are natural. Thus,
![$ L_x[r;\alpha]+L_x[r;\beta]=L_x[r;\max(\alpha,\beta)]$](img15.png) ,
,
![$ L_x[r;\alpha]L_x[r;\beta]=L_x[r;\alpha+\beta]$](img16.png) ,
,
![$ L_x[r;\alpha]L_x[s;\beta]=L_x[r;\alpha]$](img17.png) if
if 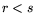 ,
,
![$ L_x[r,\alpha]^k=L_x[r,k\alpha]$](img19.png) and if
and if 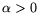 then
then
![$ (\log x)^kL_x[r;\alpha]=L_x[r;\alpha]$](img21.png) for any fixed
for any fixed 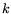 , and
, and
![$ \pi(L_x[r;\alpha])=L_x[r;\alpha]$](img23.png) where
where 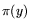 is the number of primes
is the number of primes 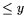 .
Let
.
Let 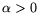 ,
,
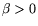 ,
, 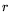 , and
, and 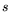 be fixed real numbers with
be fixed real numbers with
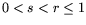 . A random
positive integer
. A random
positive integer
![$ \leq L_x[r;\alpha]$](img29.png) is
is
![$ L_x[s;\beta]$](img30.png) -smooth with
probability
-smooth with
probability
![$\displaystyle L_x[r-s;-\alpha(r-s)/\beta], $](img31.png) for
for 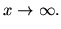
We abbreviate 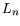 to
to 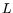 and
and
![$ L[1/3,\alpha]$](img35.png) to
to 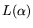 . Thus,
a random integer
. Thus,
a random integer
![$ \leq L[2/3,\alpha]$](img37.png) is
is 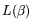 -smooth with
probability
-smooth with
probability
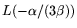 . The notation
. The notation
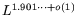 in [1] corresponds to
in [1] corresponds to
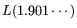 here.
We write ``
here.
We write ``
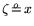 '' for ``
'' for ``
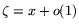 for
for
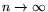 .''
.''
2.2. Ordinary NFS.
To factor 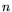 using the NFS, more or less following the approach from [11], one
selects a positive integer
for a positive value
using the NFS, more or less following the approach from [11], one
selects a positive integer
for a positive value
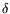 that is yet to be determined, an integer
that is yet to be determined, an integer 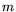 close to
close to
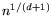 , a polynomial
, a polynomial
![$ f(X)=\sum_{i=0}^df_iX^i\in{\bf Z}[X]$](img52.png) such that
such that
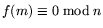 with each
with each 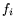 of the same order of
magnitude
as
of the same order of
magnitude
as 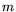 , a rational smoothness bound
, a rational smoothness bound 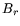 , and an algebraic smoothness
bound
, and an algebraic smoothness
bound 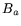 . Other properties of
these parameters are not relevant for our purposes.
A pair
. Other properties of
these parameters are not relevant for our purposes.
A pair 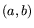 of integers is called a relation if
of integers is called a relation if 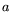 and
and 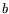 are
coprime,
are
coprime, 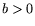 ,
, 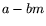 is
is 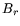 -smooth, and
-smooth, and 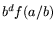 is
is 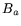 -smooth.
Each relation corresponds to a sparse
-smooth.
Each relation corresponds to a sparse 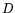 -dimensional bit vector with
-dimensional bit vector with
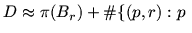 prime
prime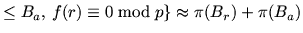
(cf. [11]).
In the relation collection step a set of more than 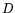 relations
is sought. Given this set, one or more linear dependencies modulo
relations
is sought. Given this set, one or more linear dependencies modulo 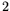 among
the corresponding
among
the corresponding 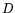 -dimensional bit vectors are constructed
in the matrix step. Per dependency there is a chance of at least 50%
(exactly 50% for RSA moduli) that
a factor of
-dimensional bit vectors are constructed
in the matrix step. Per dependency there is a chance of at least 50%
(exactly 50% for RSA moduli) that
a factor of 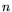 is found in the final step, the square root step. We
discuss some issues of the relation collection and
matrix steps that are relevant for [1].
is found in the final step, the square root step. We
discuss some issues of the relation collection and
matrix steps that are relevant for [1].
2.3. Relation collection.
We restrict the search for relations to the rectangle
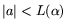 ,
,
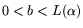 and use
and use 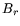 and
and 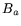 that are both
that are both 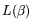 (which
does not imply that
(which
does not imply that 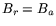 ), for
), for
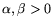 that
are yet to be determined.
It follows (cf. 2.1) that
that
are yet to be determined.
It follows (cf. 2.1) that
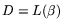 . Furthermore,
. Furthermore,
![$\displaystyle \vert a-bm\vert=L[2/3,1/\delta] $](img72.png) and
and![$\displaystyle \vert b^df(a/b)\vert=L[2/3,\alpha\delta+1/\delta].$](img73.png)
With 2.1 and under
the usual assumption that 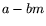 and
and 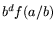 behave, with respect to
smoothness probabilities, independently as random integers of comparable
sizes, the probability that both are
behave, with respect to
smoothness probabilities, independently as random integers of comparable
sizes, the probability that both are 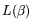 -smooth is
The search space contains
-smooth is
The search space contains
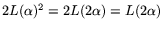 pairs
pairs
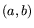 and, due to the
and, due to the 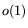 , as many pairs
, as many pairs 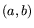 with
with
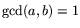 .
It follows that
.
It follows that 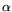 and
and 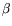 must be chosen such that
We find that
must be chosen such that
We find that
2.4. Testing for smoothness.
The 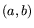 search space can be processed in
search space can be processed in
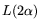 operations. If
sufficient memory is available this can be done using sieving.
Current PC implementations intended for the factorization of relatively
small
numbers usually have adequate memory for sieving. For much larger
numbers and current programs, sieving would become problematic. In that
case,
the search space can be processed in the ``same''
operations. If
sufficient memory is available this can be done using sieving.
Current PC implementations intended for the factorization of relatively
small
numbers usually have adequate memory for sieving. For much larger
numbers and current programs, sieving would become problematic. In that
case,
the search space can be processed in the ``same''
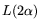 operations
(with an, admittedly, larger
operations
(with an, admittedly, larger 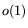 ) but at a cost of only
) but at a cost of only 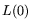 memory
using the Elliptic Curve Method (ECM) embellished in any way one sees fit
with trial division, Pollard rho, early aborts, etc., and run on any
number
memory
using the Elliptic Curve Method (ECM) embellished in any way one sees fit
with trial division, Pollard rho, early aborts, etc., and run on any
number 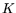 of processors in parallel to achieve a
of processors in parallel to achieve a 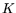 -fold speedup. This was
observed many times (see for instance [10, 4.15] and [4]).
Thus, despite the fact that current implementations of the relation collection
require substantial memory, it is well known that asymptotically this step
requires negligible memory without incurring, in theory, a runtime penalty -
in practice, however, it is substantially slower than sieving.
Intermediate solutions that exchange sieving
memory for many tightly coupled processors with small memories could prove
valuable too; see [6] for an early example of this approach
and [1] for various other interesting proposals that may turn out
to be practically relevant. For the asymptotic argument, ECM suffices.
In improved NFS from [4] it was necessary to use a
``memory-free'' method when searching for
-fold speedup. This was
observed many times (see for instance [10, 4.15] and [4]).
Thus, despite the fact that current implementations of the relation collection
require substantial memory, it is well known that asymptotically this step
requires negligible memory without incurring, in theory, a runtime penalty -
in practice, however, it is substantially slower than sieving.
Intermediate solutions that exchange sieving
memory for many tightly coupled processors with small memories could prove
valuable too; see [6] for an early example of this approach
and [1] for various other interesting proposals that may turn out
to be practically relevant. For the asymptotic argument, ECM suffices.
In improved NFS from [4] it was necessary to use a
``memory-free'' method when searching for 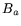 -smooth
numbers (cf. 2.2), in order to achieve the speedup.
It was suggested in [4] that the ECM may be used for this purpose.
Since memory usage was no concern for the
analysis in [4], regular ``memory-wasteful'' sieving was
suggested to test
-smooth
numbers (cf. 2.2), in order to achieve the speedup.
It was suggested in [4] that the ECM may be used for this purpose.
Since memory usage was no concern for the
analysis in [4], regular ``memory-wasteful'' sieving was
suggested to test 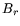 -smoothness.
-smoothness.
2.5. The matrix step.
The choices made in 2.3 result in a bit matrix 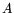 consisting of
consisting of
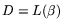 columns such that each column of
columns such that each column of 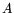 contains only
contains only 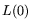 nonzero entries. Denoting by
nonzero entries. Denoting by 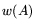 the
total number of nonzero entries of
the
total number of nonzero entries of 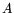 (its weight), it
follows that
(its weight), it
follows that
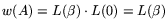 .
Using a variety of
techniques [5,13], dependencies
can be found after, essentially,
.
Using a variety of
techniques [5,13], dependencies
can be found after, essentially, 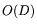 multiplications of
multiplications of 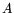 times a
bit vector. Since one matrix-by-vector multiplication can be done in
times a
bit vector. Since one matrix-by-vector multiplication can be done in
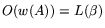 operations, the matrix step can be completed in
operations, the matrix step can be completed in
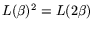 operations. We use ``standard-NFS'' to refer to NFS
that uses a matrix step with
operations. We use ``standard-NFS'' to refer to NFS
that uses a matrix step with 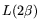 operation count.
We will be concerned with a specific method for finding the
dependencies in
operation count.
We will be concerned with a specific method for finding the
dependencies in 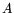 , namely the block Wiedemann algorithm
[5][18] whose outline is as follows. Let
, namely the block Wiedemann algorithm
[5][18] whose outline is as follows. Let 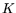 be
the blocking factor, i.e., the amount of parallelism desired. We may
assume that either
be
the blocking factor, i.e., the amount of parallelism desired. We may
assume that either 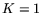 or
or 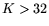 .
Choose
.
Choose 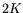 binary
binary 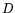 -dimensional vectors
-dimensional vectors
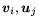 for
for
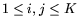 . For
each
. For
each 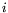 , compute the vectors
, compute the vectors
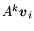 for
for 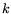 up to roughly
up to roughly 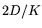 ,
using repeated matrix-by-vector multiplication. For each such vector
,
using repeated matrix-by-vector multiplication. For each such vector
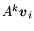 , compute the inner products
, compute the inner products
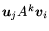 , for all
, for all
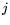 . Only these inner products are saved, to conserve storage. From
the inner products, compute certain polynomials
. Only these inner products are saved, to conserve storage. From
the inner products, compute certain polynomials 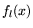 ,
,
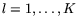 of degree about
of degree about 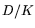 . Then evaluate
. Then evaluate
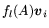 ,
for all
,
for all 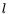 and
and 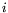 (take one
(take one 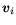 at a time and evaluate
at a time and evaluate
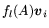 for all
for all 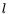 simultaneously using repeated
matrix-by-vector multiplications).
From the result,
simultaneously using repeated
matrix-by-vector multiplications).
From the result, 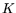 elements from the kernel of
elements from the kernel of 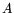 can be
computed. The procedure is probabilistic, but succeeds with high
probability for
can be
computed. The procedure is probabilistic, but succeeds with high
probability for 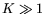 [17]. For
[17]. For 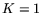 , the cost roughly
doubles [18].
For reasonable blocking factors (
, the cost roughly
doubles [18].
For reasonable blocking factors (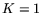 or
or
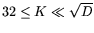 ), the block
Wiedemann algorithm involves about
), the block
Wiedemann algorithm involves about 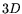 matrix-by-vector
multiplications. These multiplications dominate the cost of the matrix
step; accordingly, the circuits of [1], and our variants thereof,
aim to reduce their cost. Note that the multiplications are performed
in
matrix-by-vector
multiplications. These multiplications dominate the cost of the matrix
step; accordingly, the circuits of [1], and our variants thereof,
aim to reduce their cost. Note that the multiplications are performed
in 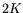 separate chains where each chain involves repeated
left-multiplication by
separate chains where each chain involves repeated
left-multiplication by 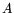 . The proposed circuits rely on this for
their efficiency. Thus, they appear less suitable for other
dependency-finding algorithms, such as block Lanczos [13]
which requires just
. The proposed circuits rely on this for
their efficiency. Thus, they appear less suitable for other
dependency-finding algorithms, such as block Lanczos [13]
which requires just 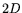 multiplications.
multiplications.
2.6. NFS parameter optimization for matrix
exponent
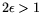 .
.
With the relation collection and matrix steps in
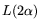 and
and
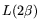 operations, respectively, the values for
operations, respectively, the values for 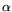 ,
, 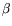 , and
, and 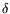 that
minimize the overall NFS operation count follow using
Relation (1).
However, we also need the optimal values if the ``cost'' of the matrix
step is different from
that
minimize the overall NFS operation count follow using
Relation (1).
However, we also need the optimal values if the ``cost'' of the matrix
step is different from
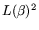 : in [1] ``cost'' is defined
using a metric that is not always the same as operation count, so we need
to analyse the NFS using alternative cost metrics. This can be done by
allowing flexibility in the ``cost'' of the matrix step: we consider how to
optimize the NFS parameters for an
: in [1] ``cost'' is defined
using a metric that is not always the same as operation count, so we need
to analyse the NFS using alternative cost metrics. This can be done by
allowing flexibility in the ``cost'' of the matrix step: we consider how to
optimize the NFS parameters for an
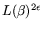 matrix step, for some exponent
matrix step, for some exponent
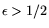 . The corresponding relation collection operation count
is fixed at
. The corresponding relation collection operation count
is fixed at
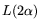 (cf. 2.4).
We balance the cost of the relation collection and matrix steps by taking
(cf. 2.4).
We balance the cost of the relation collection and matrix steps by taking
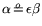 . With (1) it follows that
. With (1) it follows that
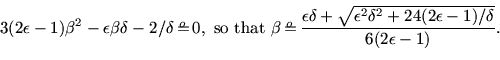
Minimizing 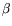 given
given 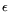 leads to
leads to
and
Minimizing the resulting
leads to
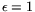 and
and
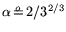 : even though
: even though
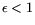 would allow more ``relaxed'' relations (i.e., larger smoothness bounds and
thus easier to find), the fact that more of such relations have to be found
becomes counterproductive. It follows that an operation count of
would allow more ``relaxed'' relations (i.e., larger smoothness bounds and
thus easier to find), the fact that more of such relations have to be found
becomes counterproductive. It follows that an operation count of
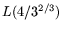 is optimal for relation collection, but that for
is optimal for relation collection, but that for
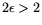 it is better to use suboptimal relation collection because otherwise the
matrix step would dominate. We find the following optimal NFS parameters:
it is better to use suboptimal relation collection because otherwise the
matrix step would dominate. We find the following optimal NFS parameters:
-
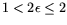 :
:

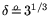 ,
,
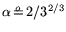 , and
, and
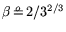 , with operation counts of relation collection and
matrix steps equal to
, with operation counts of relation collection and
matrix steps equal to
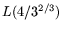 and
and
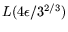 , respectively. For
, respectively. For
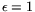 the operation counts of the two steps are the same (when expressed in
the operation counts of the two steps are the same (when expressed in 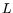 )
and the overall operation count is
)
and the overall operation count is
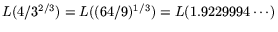 .
This corresponds to the heuristic asymptotic runtime of the NFS as given
in [11]. We refer to these parameter choices as the ordinary
parameter choices.
.
This corresponds to the heuristic asymptotic runtime of the NFS as given
in [11]. We refer to these parameter choices as the ordinary
parameter choices.
-
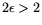 :
:

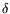 ,
, 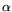 , and
, and 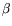 as given by Relations (2),
(4), and (3), respectively, with operation count
as given by Relations (2),
(4), and (3), respectively, with operation count
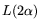 for relation collection and cost
for relation collection and cost
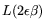 for the matrix step, where
for the matrix step, where
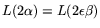 . More in
particular, we find the following values.
. More in
particular, we find the following values.
-
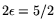 :
:

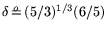 ,
,
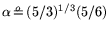 , and
, and
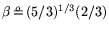 , for an operation count and cost
, for an operation count and cost
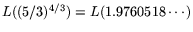 for the relation collection and matrix
steps, respectively. These values are
familiar from [1, Section 6: Circuits].
With
for the relation collection and matrix
steps, respectively. These values are
familiar from [1, Section 6: Circuits].
With
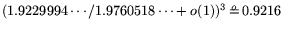 and equating
operation count and cost, this suggests that factoring
and equating
operation count and cost, this suggests that factoring
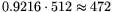 -bit composites using NFS with matrix
exponent
-bit composites using NFS with matrix
exponent 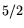 is comparable to factoring 512-bit ones using standard-NFS
with ordinary parameter choices (disregarding the effects of the
is comparable to factoring 512-bit ones using standard-NFS
with ordinary parameter choices (disregarding the effects of the 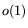 's).
's).
-
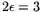 :
:

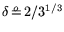 ,
,
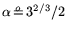 , and
, and
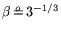 , for
an operation count and cost of
, for
an operation count and cost of
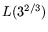
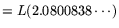 for the
relation collection and matrix steps, respectively.
for the
relation collection and matrix steps, respectively.
2.7. Improved NFS.
It was shown
in [4] that ordinary NFS from [11], and as used
in 2.2, can be improved by using more than a single polynomial 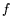 .
Let
.
Let 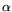 and
and 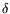 be as in 2.3 and 2.2,
respectively, let
be as in 2.3 and 2.2,
respectively, let 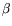 indicate the rational smoothness bound
indicate the rational smoothness bound 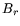 (i.e.,
(i.e.,
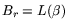 ), and let
), and let 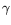 indicate the algebraic smoothness
bound
indicate the algebraic smoothness
bound 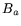 (i.e.,
(i.e.,
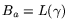 ). Let
). Let 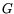 be a set of
be a set of
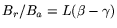 different polynomials, each of degree
different polynomials, each of degree 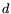 and
common root
and
common root 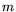 modulo
modulo 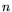 (as in 2.2). A pair
(as in 2.2). A pair 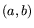 of
integers is a relation if
of
integers is a relation if 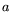 and
and 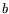 are coprime,
are coprime, 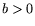 ,
, 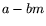 is
is
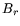 -smooth, and
-smooth, and 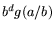 is
is 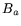 -smooth for at least one
-smooth for at least one 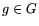 .
Let
.
Let 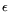 be the matrix exponent. Balancing the cost of the relation
collection and matrix steps it follows that
be the matrix exponent. Balancing the cost of the relation
collection and matrix steps it follows that
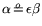 .
Optimization leads to
.
Optimization leads to
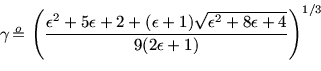
and for this 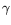 to
to
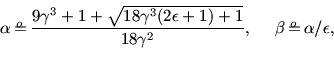
and
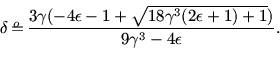
It follows that for
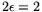 the method from [4]
gives an improvement over the ordinary method, namely
the method from [4]
gives an improvement over the ordinary method, namely
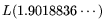 . The condition
. The condition
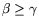 leads to
leads to
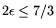 , so that for
, so that for
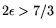 (as in circuit-NFS,
cf. 3.1) usage of the method from [4] no
longer leads to an improvement over the
ordinary method. This explains why in [1] the method from [4]
is used to select parameters for standard-NFS and why the ordinary method
is used for circuit-NFS.
With 2.1 it follows that the sum of the (rational) sieving
and ECM-based (algebraic) smoothness times from [4] (cf. last
paragraph of 2.4) is minimized if
(as in circuit-NFS,
cf. 3.1) usage of the method from [4] no
longer leads to an improvement over the
ordinary method. This explains why in [1] the method from [4]
is used to select parameters for standard-NFS and why the ordinary method
is used for circuit-NFS.
With 2.1 it follows that the sum of the (rational) sieving
and ECM-based (algebraic) smoothness times from [4] (cf. last
paragraph of 2.4) is minimized if
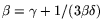 .
The above formulas then lead to
.
The above formulas then lead to
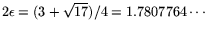 . Therefore, unlike the ordinary
parameter selection method, optimal relation collection for the improved
method from [4] occurs for an
. Therefore, unlike the ordinary
parameter selection method, optimal relation collection for the improved
method from [4] occurs for an 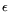 with
with
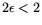 : with
: with
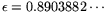 the operation count for relation collection becomes
the operation count for relation collection becomes
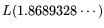 . Thus, in principle, and
depending on the cost function one is using, the improved method would
be able to take advantage of a matrix step with exponent
. Thus, in principle, and
depending on the cost function one is using, the improved method would
be able to take advantage of a matrix step with exponent
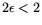 .
If we disregard the matrix step and minimize the
operation count of relation collection, this method yields a cost of
.
If we disregard the matrix step and minimize the
operation count of relation collection, this method yields a cost of
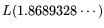 .
.


Next: The circuits for integer
Up: Analysis of Bernstein's Factorization
Previous: Introduction