


Next: Hardware for the matrix
Up: Analysis of Bernstein's Factorization
Previous: The circuits for integer
Subsections
Operation count, equipment cost, and real time
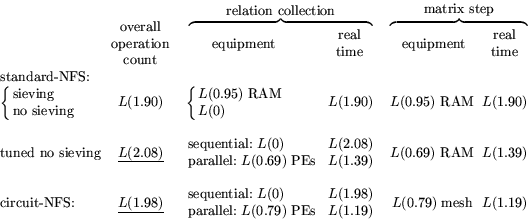
The asymptotic characteristics of standard-NFS and circuit-NFS with respect
to
their operation count, equipment, and real time spent are summarized in
Table 1. For non-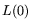 equipment requirements it is
specified if the main cost goes to memory (``RAM''), processing elements
(``PEs'')
with
equipment requirements it is
specified if the main cost goes to memory (``RAM''), processing elements
(``PEs'')
with 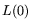 memory, or a square mesh as in 3.1, and ``tuned''
refers to the alternative analysis in 3.6. The underlined
operation counts are the same as the corresponding throughput costs. For
the other operation count the throughput cost (not optimized if no
sieving is used) follows by taking the maximum of the products of the
figures in the ``equipment'' and ``real time'' columns.
Relation collection, whether using sieving or not, allows almost arbitrary
parallelization (as used in the last two rows of Table 1).
The amount of parallelization allowed in the matrix step of standard-NFS is
much more limited (cf. 2.5); it is not used in
Table 1.
memory, or a square mesh as in 3.1, and ``tuned''
refers to the alternative analysis in 3.6. The underlined
operation counts are the same as the corresponding throughput costs. For
the other operation count the throughput cost (not optimized if no
sieving is used) follows by taking the maximum of the products of the
figures in the ``equipment'' and ``real time'' columns.
Relation collection, whether using sieving or not, allows almost arbitrary
parallelization (as used in the last two rows of Table 1).
The amount of parallelization allowed in the matrix step of standard-NFS is
much more limited (cf. 2.5); it is not used in
Table 1.
Table 1:
NFS costs: operation count, equipment, and real
time.
|
4.1. Lowering the cost of the standard-NFS matrix step.
We show at what cost the asymptotic
advantages of the circuit-NFS matrix step (low throughput cost and
short real time) can be matched, asymptotically, using the traditional
approach to the matrix step. This requires a smaller matrix, i.e., lower
smoothness bounds, and results therefore in slower relation collection. We
illustrate this with two examples. To get matching throughput
costs for the matrix steps of standard-NFS
and circuit-NFS, 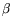 must be chosen such that
must be chosen such that
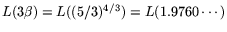 , so that the matrix step of
standard-NFS requires
, so that the matrix step of
standard-NFS requires
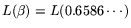 RAM
and real time
RAM
and real time
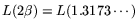 .
Substituting this
.
Substituting this 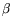 in Relation (1) and minimizing
in Relation (1) and minimizing 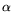 with respect to
with respect to 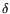 we find
we find
i.e.,
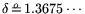 and
and
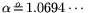 , resulting in
relation collection operation count
, resulting in
relation collection operation count
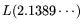 . Or, one
could match the real time of the matrix steps:
with
. Or, one
could match the real time of the matrix steps:
with
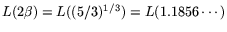 the
matrix step of standard-NFS requires
the
matrix step of standard-NFS requires
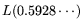 RAM
and real time
RAM
and real time
 . With Relation (5)
we find that
. With Relation (5)
we find that
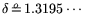 ,
,
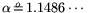 , and
relation collection operation count
, and
relation collection operation count
 .
.
4.2. Operation count based estimates.
Operation count is the traditional way of measuring the cost of the NFS.
It corresponds to the standard complexity measure of ``runtime'' and
neglects
the cost of memory or other equipment that is needed to actually ``run'' the
algorithm. It was used, for instance, in [11] and [4]
and was analysed in 2.6 and 2.7.
It can be seen in Table 1, and was
indicated in 3.5, that the operation count for circuit-NFS is
higher than for standard-NFS (assuming both methods are optimized
with respect to the operation count):
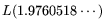 as opposed
to just
as opposed
to just
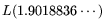 when using the improved version
(cf. 2.7) as in Table 1, or as opposed to
when using the improved version
(cf. 2.7) as in Table 1, or as opposed to
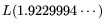 when using the ordinary version (cf. 2.6)
as in 3.5. Thus, RSA moduli that are deemed
sufficiently secure based on standard-NFS operation count security
estimates, are even more secure when circuit-NFS is considered instead.
Such estimates are common; see for instance [14] and the
``computationally equivalent'' estimates in [9,12].
Security estimates based on the recommendations from [14] or
the main ones (i.e., the conservative ``computationally equivalent'' ones)
from [9,12] are therefore not affected by the result
from [1]. Nevertheless, we agree with [2] that the
PC-based realization suggested in [12], meant to present an
at the time possibly realistic approach that users can relate to, may not be
the best way to realize a certain operation count; see also the
last paragraph of [12, 2.4.7].
The estimates from [15] are affected by [1].
when using the ordinary version (cf. 2.6)
as in 3.5. Thus, RSA moduli that are deemed
sufficiently secure based on standard-NFS operation count security
estimates, are even more secure when circuit-NFS is considered instead.
Such estimates are common; see for instance [14] and the
``computationally equivalent'' estimates in [9,12].
Security estimates based on the recommendations from [14] or
the main ones (i.e., the conservative ``computationally equivalent'' ones)
from [9,12] are therefore not affected by the result
from [1]. Nevertheless, we agree with [2] that the
PC-based realization suggested in [12], meant to present an
at the time possibly realistic approach that users can relate to, may not be
the best way to realize a certain operation count; see also the
last paragraph of [12, 2.4.7].
The estimates from [15] are affected by [1].
Remark 4.3
Historically, in past factorization experiments the matrix step
was always solved using a fraction of the effort required by
relation collection. Moreover, the memory requirements of
sieving-based relation collection have never turned out to be a
serious problem (it was not even necessary to fall back to the
memory-efficient ECM and its variations). Thus, despite the
asymptotic analysis, extrapolation from past experience would
predict that the bottleneck of the NFS method is relation
collection, and that simple operation count is a better practical
cost measure for NFS than other measures that are presumably more
realistic. The choice of cost function in [9,12] was
done accordingly.
The findings of [1] further support this conservative approach,
by going a long way towards closing the gap between the two measures
of cost when applied to the NFS: 93% of the gap according
to 3.5, and 61% according to 3.6.



Next: Hardware for the matrix
Up: Analysis of Bernstein's Factorization
Previous: The circuits for integer
